CBSE Sample Papers for Class 10 Maths Basic Set 3 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Basic with Solutions Set 3 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Basic Set 3 with Solutions

Time : 3 hrs
Max. Marks : 80

General Instructions:

1. This Question Paper has 5 Sections A, B, C, D and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answer-I (SA-I) type questions carrying 2 marks each.
4. Section C has 6 Short Answer-II (SA-II) type questions carrying 3 marks each.
5. Section D has 4 Long Answer (LA) type questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment questions (4 marks each).
7. All Questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks and 2 Questions of 5 marks has been provided. An internal choice has been provided in the 2 marks question of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section – A
Section A consists of 20 questions of 1 mark each

Question 1.
The median of the data 12, 15, 17, 19, 22, 27 is
(a) 17
(b) 18
(c) \(\frac{41}{2}\)
(d) 19
Answer:
(b) 18

For the given data, these are two middle terms, 17 and 19.
∴ Median = \(\frac{17+19}{2}\)
= \(\frac{36}{2}\) = 18

Question 2.
The value of c for which pair of linear equations cx – y = 2 and 6x – 2y = 4 will have infinitely many solutions is: 1
(a) 3
(b) 5
(c) -1
(d) 0
Answer:
(a) 3
Explanation: We have
cx – y = 2 and
6x – 2y = 4
For infinitely many solutions
\(\frac{c}{6}=\frac{-1}{-2}=\frac{2}{4}\)
\(\frac{c}{6}=\frac{1}{2}\)
⇒ c = 3

Question 3.
The HCF of two numbers is 116 and their LCM is 1740. If one number is 580, then the other number is
(a) 580
(b) 348
(c) 680
(d) 448
Answer:
(b) 348

Let the other number be y, then.
(1 st number × the other number) = HCF × LCM
580 × y = 116 × 1740
y = \(\frac{116 \times 1740}{580}\) = 348

Question 4.
School divides its students into 5 houses A,B, C, D and E. Class X A has 23 students, 4 from house A, 8 from house B, 5 from house C, 2 from house D and rest from house E. A single student is chosen randomly to become the class monitor. The probability that the chosen student is not from houses A, B and C is: 1
(a) \(\frac{4}{23}\)
(b) \(\frac{6}{23}\)
(c) \(\frac{8}{23}\)
(d) \(\frac{17}{23}\)
Answer:
(b) \(\frac{6}{23}\)
Explanation: Total students in class X = 23
Students from house A = 4
Students from house B = 8
Students from house C = 5
Students from house D = 2
Students from house E = 23 – (4 + 8 + 5 + 2) = 4
Total students in houses D and E = 2 + 4 = 6
Required probability = \(\frac{6}{23}\)

Question 5.
If we join two hemispheres of same radius along their bases, then we get a
(a) cone
(b) cylinder
(c) cuboid
(d) sphere
Answer:
(d) Sphere

Question 6.
If ΔABC ~ ΔDEF, such that ∠A = 47° and ∠E = 83°, then the value of ∠C is: 1

(a) 50°
(b) 60°
(c) 45°
(d) 90°
Answer:
(a) 50°
Explanation: Since ΔABC ~ ΔDEF.
∠A = ∠D, ∠B = ∠E and ∠C = ∠F
⇒ ∠A = 47° and ∠B = 83°
So, in ΔABC, ZC = 180° – (∠A + ∠B)
= 180° – (47° + 83°)
= 50°

Question 7.
If x cot 45° cos 60° = sin 30° sin 90°, then the value of x is
(a) \(\frac{1}{2}\)
(b) – 1
(c) 1
(d) 2
Answer:
(c) 1

We have, x cot45° cos 60° = sin30° sin90°
∴ x × 1 × \(\frac{1}{2}\) = \(\frac{1}{2}\) × 1
⇒ x = 1

Question 8.
If cot A + \(\frac{1}{\cot A}\) = 2, then the value of cot ² A + \(\frac{1}{\cot ^2 A}[latex], is: 1
(a) 2
(b) 4
(c) 1
(d) 5
Answer:
(a) 2
Explanation:
Given, cot A + [latex]\frac{1}{\cot A}\) = 2
On squaring both sides, we get

Question 9.
In an ∆ABC, it is given that AB = 6 cm, AC = 8 cm and AD is the bisector of ∠A, then BD : DC is

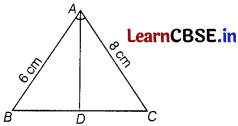
(a) 3 : 4
(b) 4 : 3
(c) 9 : 16
(d) √3 : 2
Answer:
(a) 3 : 4

We know that \(\frac{B D}{D C}=\frac{A B}{A C}\)
= \(\frac{6}{8}=\frac{3}{4}\)

Question 10.
If sin A = \(\frac{1}{2}\),then the value of(cotA – cosA)is: 1
(a) √3
(b) \(\frac{1}{\sqrt{3}}[latex]
(c) [latex]\frac{3}{2}\)
(d) \(\frac{\sqrt{3}}{2}\)
Answer:
(d) \(\frac{\sqrt{3}}{2}\)
Explanation:
sin A = \(\frac{1}{2}\) gives A = 30°
So, cot A – cos A = cot 30° – cos 30°
= √3 – \(\frac{\sqrt{3}}{2}\) = \(\frac{\sqrt{3}}{2}\)

Question 11.
The product of the zeroes of the polynomial, 6x ² – 4x + 9 is
(a) – \(\frac{1}{2}\)
(b) – \(\frac{3}{2}\)
(c) \(\frac{3}{2}\)
(d) \(\frac{1}{2}\)
Answer:
(c) \(\frac{3}{2}\)

Let P(x) = 6x ² – 4x + 9
Now product of zeroes = \(\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)
= \(\frac{9}{6}=\frac{3}{2}\)

Question 12.
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 45°, The height of the tower (in metres) is: 1
(a) 15
(b) 30
(c) 30√3
(d) 10√3
Answer:
(b) 30
Explanation: Let AB be the tower and P be the point on the ground.

In ΔABP, \(\frac{\mathrm{AB}}{\mathrm{BP}}\) = tan 45°
⇒ \(\frac{\mathrm{AB}}{30}\) = 1
⇒ AB = 30 m

Question 13.
The coordinates of A and B are (- 3, a) and (1, a + 4). If the mid-point of AB is (- 1, 1), then the value of a is
(a) 0
(b) – 1
(c) – \(\frac{1}{2}\)
(d) 1
Answer:
(b) – 1

Mid-point of AB = \(\left(\frac{-3+1}{2}, \frac{a+a+4}{2}\right)\)
= (- 1, 1)
⇒ (- 1, a + 2) = (- 1, 1)
⇒ a + 2 = 1
⇒ a = – 1

Question 14.
What is the upper limit of the median class for the given below distribution? 1

Class Interval	Frequency
0 – 5	13
5 – 10	10
10 – 15	15
15 – 20	8
20 – 25	11

(a) 14
(b) 10
(c) 15
(d) 20
Answer:
(c) 15
Explanation:

Here, N = 57
So, \(\frac{N}{2}\) = 28.5
Cumulative frequency just greater than 28.5 is 38, which belongs to 10 – 15.
So, the median class is 10 – 15.
Thus, its upper limit is 15.

Question 15.
The distance between the points A (9, 3) and B (15, 15) is
(a) 6√5 units
(b) 2√5 units
(c) 3√5 units
(d) 3√3 units
Answer:
(a) 6√5 units

We know that d = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
= \(\sqrt{(15-9)^2+(15-3)^2}\)
= \(\sqrt{(6)^2+(12)^2}\)
= \(\sqrt{36+144}\)
= \(\sqrt{180}\)
= 6√5 units

Question 16.
The common difference of the AP., √3, \(\sqrt{12}\), \(\sqrt{27}\) ……………….. is: 1
(a) \(\sqrt{12}\)
(b) √4
(c) √3
(d) 2√3
Answer:
(c) √3
Explanation: Here the terms of the A.P. are:
√3, 2√3, 3√3,…….
So, the common difference = (2√3 – √3) = √3.

Question 17.
Two concentric circles are of radii 17 cm and 8 cm. Then, the length of the chord of the larger circle which touches the smaller circle is
(a) 16 cm
(b) 36 cm
(c) 15 cm
(d) None of these
Answer:
(d) None of these

Let O be the centre of concentric circles of radii 17 cm and 8 cm, respectively.

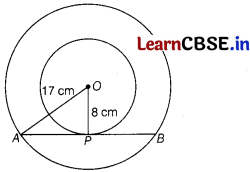
Let AB be a chord of the larger circle touching the smaller circle at P.
Then, AP = PS and OP ⊥ AB.
Now, in ∆OPA, we have
OA ² = OP ² + AP ² [by Pythagoras theorem]
⇒ (17) ² = (8) ² + AP ²
⇒ 289 = 64 + AP ²
⇒ AP ² = 225
⇒ P = 15 cm
∴ AB = 2AP
= 2 × 15 = 30 cm

Question 18.
The arithmetic mean of the following frequency distribution is: 1

Class interval	Frequency
0 – 10	5
10 – 20	18
20 – 30	15
30 – 40	16
40 – 50	6

(a) 25
(b) 37
(c) 45
(d) 22
Answer:
(a) 25
Explanation: Now, the frequency distribution table from the given data can be drawn as:

Directions: In question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.

Question 19.
Assertion (A) : In a circle of radius 6 cm, the angle of a sector is 60°, then the area of the sector is \(\frac{132}{7}\) cm ² .
Reason (R) : Area of the circle with radius r is πr ² .
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).

Area of a sector = \(\frac{\theta}{360^{\circ}}\) × πr²
Here, θ = 60° and r = 6 cm
∴ Area of given sector = \(\frac{60^{\circ}}{360^{\circ}} \times \frac{22}{7}\) × 6 × 6
= \(\frac{22 \times 6}{7}\)
= \(\frac{132}{7}\) cm ²
So, the Assertion (A) is true.
Area of a circle with radius, r = πr²
Reason (R) is also true but it is not the correct explanation of Assertion (A).

Question 20.
Assertion (A): The simplest form of \(\frac{1095}{1168}\) is \(\frac{15}{16}\)
Reason (R): For finding the simplest form of a fraction the numerator and denominator are divided by their HCF. 1
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A)
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A)
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Answer:
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A)
Explanation: Here, the HCF of 1095 and 1168 is 73.
\(\frac{1095 \div 73}{1168 \div 73}=\frac{15}{16}\), is the simplest form of fraction.

Section – B
Section B consists of 5 questions of 2 marks each

Question 21.
The length of minute hand of a clock is a 28 cm. Find the area swept by the minute hand in 1 min.
Answer:
The minute hand of a clock describes a circle of radius equal to its length
i.e. 28 cm in 1 h.
So, the angle described by minute hand in 60 min = 360°
∴ Angle described by minute hand in 1 min = \(\frac{360}{60}\) = 6°
So, the area swept by the minute hand in 1 min is the area of a sector of angle 6° in a circle of radius 28 cm
Required area = \(\frac{\theta}{360^{\circ}}\) πr²
= \(\frac{6^{\circ}}{360^{\circ}} \times \frac{22}{7}\) × (28) ²
= \(\frac{6^{\circ}}{360^{\circ}} \times \frac{22}{7}\) × 28 × 28
= 41.06 cm

Question 22.
Find the area of the shaded region in the given figure, if ABCD is a square of side 20 m and APD and BPC are semicircles. (Use π = \(\frac{22}{7}\)) 2

Answer:
Area of semicircle BPC
\(\frac{1}{2}\)πr ² = \(\frac{1}{2}\)π × (10) ²
= 50π m ²
Similarly

Area of semicircle APD = 50π m ²
Total area of semicircle BPC and APD
= (50π + 50π)m ²
= 100π m ² = 100 × \(\frac{22}{7}\)
= \(\frac{2200}{7}\)m ²
Side of square = 20 m
∴ Area of the square ABCD
= 20 × 20 = 400 m ²
∴ Area of the shaded region = (Area of square Area of both semicircles BPC and APD)
= (400 – \(\frac{2200}{7}\))m ²
= \(\frac{600}{7}\)m ²

Question 23.
Without solving the following quadratic equation, find the value of p for which the roots are equal px ² – 9x – 6 = 0
Answer:
Given, quadratic equation is px ² – 9x – 6 = 0
On comparing it with ax ² + bx + c = 0, we get
a = p,
b = – 9
and c = – 6
Since the given equation has equal roots.
So, the discriminant D will be zero.
∴ D = b ² – 4ac = 0
⇒ (- 9) ² – 4 × p × (- 6) = 0
⇒ 81 + 24p = 0
⇒ 24p = – 81
⇒ p = \(\frac{-81}{24}\)
= \(\frac{-27}{8}\)

Question 24.
A path of width 7 m runs around outside a circular park whose radius is 18 m. Find the area of the path. 2
Answer:
Given, radius = 18 m
Area of the path = Area of the outer circle – Area of the inner circle
= [π(18 + 7) ² – π(18) ² ] sq. m

= (625π – 324π) sq. m
= 301π sq. m, or 946 sq. m.

Question 25.
Find the 25th term of the AP – 5, \(\frac{-5}{2}\), 0, \(\frac{5}{2}\), ……………
Answer:
Given, AP is – 5, \(\frac{-5}{2}\), 0, \(\frac{5}{2}\), ……………
Here, a = – 5
and common difference (d) = \(\frac{-5}{2}\) – (- 5)
= \(\frac{-5}{2}\) + 5 = \(\frac{5}{2}\)
25th term of the given AP is
a ₂₅ = a + (25 – 1) d
[∵ a _n = a + (n – 1) d]
⇒ a ₂₅ = – 5 + 24 (\(\frac{5}{2}\))
= – 5 + 60 = 55
Hence, 25th term of the given AP is 55.

Or

Determine the AP, whose 3rd term is 5 and the 7th term is 9.
Answer:
Let a and d be the first term and common difference of an AP
∴ T ₃ = 5
and T ₇ = 9
⇒ a + (3 – 1) d = 5
[∵ a _n = a + (n – 1) d]
and a + (7 – 1) d = 9
⇒ a + 2d = 5 …………..(i)
and a + 6d = 9 ………….(ii)
On subtracting Eq. (I) from Eq. (ii), we get
6d – 2d = 9 – 5
4d = 4
⇒ d = 1
On putting d = 1 in Eq. (I), we get
a + 2 × 1 = 5
⇒ a = 3
∴ The required AP is 3, 4, 5, 6, ………….

Section – C
Section C consists of 6 questions of 3 marks each

Question 26.
Amita, Suneha, and Rajiv start preparing cards. To complete one card, they take 10, 16, and 20 minutes respectively, If all of them started together, after what time will they start preparing a new card together?
OR
Show that 5 + 2√7 is an irrational number, where √7 is given to be an irrational number. 3
Answer:
Given, Amita, Suneha and Rajiv takes 10, 16 and 20 minutes respectively to complete one card.
Prime factorisation of 10,16 and 20 is 10 = 2 × 5, 16 = 2 × 2 × 2 × 2 = 2 ⁴ and 20 = 2 × 2 × 5 = 2 ² × 5
∴ Time after which they start preparing a new card together = LCM (10, 16 and 20)
= 2 × 2 × 2 × 2 × 5
= 2 ⁴ × 5 = 80 minutes.
OR
Suppose 5 + 2√7 is a rational number.
∴ We can find two integers a, b ( b ≠ 0) such that 5 + 2√7 = \(\frac{a}{b}\), where a and b are co-prime integers.
⇒ 2√7 = \(\frac{a}{b}\) – 5
⇒ √7 = \(\frac{1}{2}\)[\(\frac{a}{b}\) – 5]
⇒ √7 is a rational number
[∵ a, b are integers, so \(\frac{1}{2}\)[\(\frac{a}{b}\) – 5] number] is a rational number
But this contradicts the fact that √7 is an irrational number. Hence, our assumption is wrong. Thus, 5 + 2√7 is an irrational number.

Question 27.
Solve (x – 3) (x – 4) = \(\frac{34}{(33)^2}\)
Answer:
(x – 3) (x – 4) = \(\frac{34}{(33)^2}\)
x ² – 7x + 12 – \(\frac{34}{(33)^2}\) = 0
x ² – 7x + \(\frac{13034}{(33)^2}\) = 0

Question 28.
ABCD is a quadrilateral such that ∠D = 90°, A circle C(O, r) touches the sides AB, BC, CD, and DA at P, Q, R, and S respectively. If BC = 38 cm, CD = 25 cm, and BP = 27 cm, then find the value of r.
OR
In the given figures, ∠DAB = 90°, AD = 40 cm, CD = 35 cm, and CQ = 18 cm. Find the radius of the circle.

Answer:
Since, tangents drawn from an external point to a circle are equal.

∴ AP = AS, BP = BQ, CQ = CR,
DS = DR
BP = 27 cm
⇒ BQ = 27 cm
Now, CQ = BC – BQ
= 38 – 27
= 11 cm
⇒ CR = 11 cm
DR = DC – CR
= 25 – 11 = 14 cm
Now, OR ⊥ CD and OS ⊥ AD
[∴ Tangent at any point of a circle is perpendicular to the radius through the point of contact.] and OS = OR [Radii of same circle]
Also, given that ∠D = 90°
∴ ORDS is a square of side 14 cm.
Thus, radius of circle is 14 cm.
OR
Join OP and OS.
Since length of tangents drawn from an external point to a circle are equal
∴ AP = AS [Tangents from A] …… (i)
CQ = CR [Tangents from C] ,…… (ii)
DR = DS [Tangents from D] ……..(iii)

Now,
CQ = CR
⇒ CR = 18 cm [∵ CQ = 18 cm (given)]
DR = DC – CR = 35 – 18 = 17 cm [∵ CD = 35 cm (given)]

∴ DS = 17 cm [Using (iii)]
AS = AD – DS = 40 – 17 = 23 cm [∵ AD = 40 cm (given)]
∴ AP = 23 cm [Using (i)]
Now, OP ⊥ AP and OS ⊥ AS
[∵ Tangent at any point of circle is perpendicular to the radius through the point of contact]
Also, ∠DAB = 90° [Given]
Since, all angles are of 90° and adjacent sides are equal in APOS, So APOS is a square.
OP = OS = AS = AP
= 23 cm.
Thus, radius of the circle is 23 cm.

Question 29.
Ram started work in year 1995 at an annual salary of ₹ 5000 and received a ₹ 200 raise each year. In what year did his annual salary will reach ₹ 7000?
Answer:
Annual salary received by Ram in 1995, 1996, 1997 ……….. is ₹ 5000, ₹ 5200, ₹ 5400.
Clearly, it is AP with first term, a = 5000
and common difference, d = 5200 – 5000 = 200
Suppose Ram’s annual salary reaches to ₹ 7000 in nth yr.
Then, nth term of the above AP
T _n = ₹ 7000
∴ a + (n – 1) d = T _n
⇒ 5000 + (n – 1) × 200 = 7000
⇒ (n – 1) × 200 = 2000
⇒ n – 1 = \(\frac{2000}{200}\) = 10
⇒ n = 10 + 1 = 11
Thus, 11th annual salary received by Ram will be ₹ 7000.
This means that after 10yr i.e. in the year 2005 his annual salary will reach to ₹ 7000.

Question 30.
If sin A = m sin B and tan A = n tan B then show that (n ² – 1) cos ² A = m ² – 1. 3
Answer:
Given: tan A = n tan B
and sin A = m sin B
To Prove:
(n ² – 1) cos ² A = m ² – 1
Proof sin A = m sin B (given) ……… (i)
tan A = n tan B
\(\frac{\sin A}{\cos A}\) = n\(\frac{\sin B}{\cos B}\) ………… (ii)
On substituting sin B from eq. (i), we get
⇒ cos B = \(\frac{n}{m}\) cos A ………. (iii)
and sin ² A = m ² sin ² B
⇒ (1 – cos ² A) = m ² (1 – cos ² B)
Substituting cos B from eq. (iii), we get
1 – cos ² A = m ² (1 – \(\frac{n^2}{m^2}\)cos ² A)
⇒ 1 – cos ² A = m ² (\(\frac{m^2-n^2 \cos ^2 \mathrm{~A}}{m^2}\))
1 – cos ² A = m ² – n ² cos ² A
n ² cos ² A – COS ² A = m ² – 1
cos ² A (n ² – 1) = m ² – 1
Hence, proved.

Question 31.
Find the ratio in which the point P (x, 2) divides the line segment joining the points A (12, 5) and B(4, – 3). Also, find the value of x.
Answer:
Let the required ratio be k : 1.
Then, by section formula,
P = \(\left(\frac{4 k+12}{k+1}, \frac{-3 k+5}{k+1}\right)\)
But this point is given as P(x, 2).
On comparing, we get
\(\frac{4 k+12}{k+1}\) = x ………….(i)
and \(\frac{-3 k+5}{k+1}\) = 2 …………(ii)
From Eq( ii),
\(\frac{-3 k+5}{k+1}\) = 2
⇒ – 3k + 5 = 2k + 2
⇒ 5k = 3
⇒ k = \(\frac{3}{5}\)
So, the rabo is 3 : 5,
On putting, k = \(\frac{3}{5}\) in Eq. (i), we get
x = \(\frac{\left(4 \times \frac{3}{5}+12\right)}{\left(\frac{3}{5}+1\right)}\)
= \(\frac{72}{8}\) = 9
Hence, x = 9.

Section – D
Section D consists of 4 questions of 5 marks each

Question 32.
Solve the pair of equations graphically:
4x – y = 5; x + y = 5.
OR
Form a pair of linear equations for the following problems and find their ‘ solution by substitution method.
(A) The cost of a taxi in a city consists of a fixed charge and a charge for the distance travelled. The cost for a 10 km travel is ₹ 105, while for a 15 km journey, the cost is ₹ 155. What are the fixed charges and the km charged? How much will it cost someone to drive 25 km?
(B) For ₹ 3800, the cricket team’s coach purchases 6 balls and 7 bats. Then he spends 1750 for 3 bats and 5 balls. Find out how much each ball and bat costs. 5
Answer:
4x – y = 5

x	1	2
y	-1	3

x + y = 5

x	3	2
y	2	3

The solution is x = 2, y = 3.
OR
(A) Let fixed charge = ₹ x and let charge for every km = ₹ y
According to given conditions, we have
x + y = 105 ………… (i)
x + 15y = 155 …………… (ii)
Using equation (i), we can say that
x = 105 – 10y
Putting this in equation (ii), we get
105 – 10y + 15y = 155
⇒ 5x = 50
⇒ y = 10
Putting value of y in equation (i), we get
x + 10(10) = 105
⇒ x = 105 – 100
⇒ x = 5
Therefore, fixed charge = ₹ 5
and charge per km = ₹ 10
To travel distance of 25 km, person will have to pay = ₹ (x + 25y)
= ₹ (5 + 25 × 10)
= ₹ (5 + 250)
= ₹ 255

(B) Let cost of each bat = ₹ x
and cost of each ball = ₹ y
According to given conditions, we have
7x + 6y = 3800 …………. (i)
And, 3x + 5 y = 1750 …………. (ii)
Using equation (i), we can say that
7x = 3800 – 6y
⇒ x = \(\frac{3800-6 y}{7}\)
Putting this in eq. (ii), we get “3800-6y’
3(\(\frac{3800-6 y}{7}\)) + 5y = 1750
⇒ (\(\frac{11400-18 y}{7}\)) + 5y = 1750
⇒ \(\frac{5 y}{1}-\frac{18 y}{7}=\frac{1750}{1}-\frac{11400}{7}\)
⇒ \(\frac{35 y-18 y}{7}=\frac{12250-11400}{7}\)
⇒ 17 y = 850
⇒ y = 50
Putting value of y in (ii), we get
3x + 250 = 1750
⇒ 3x = 1500
⇒ x = 500
Therefore, cost of each bat = ₹ 500 and
cost of each ball = ₹ 50.

Question 33.
A card is drawn from a well-shuffled pack of 52 cards. Find the probability that the card drawn is
(i) 5 of heart or diamond
(ii) jack or queen
(iii) ace and king
(iv) a red or a king
Answer:
A card is drawn from a well-shuffled pack of 52 cards.
∴ Number of possible outcomes = 52

(i) There are 2 such cards (5 of heart and 5 of diamond).
∴ P (drawn card is 5 of heart or diamond) = \(\frac{2}{52}=\frac{1}{26}\)

(ii) There are total 8 such cards (4 jack and 4 queen).
∴ P (drawn card is a jack or queen) = \(\frac{8}{52}=\frac{2}{13}\)

(iii) There is no card, which is an ace as well as king.
∴ P (drawn card is ace and king) = \(\frac{0}{52}\) = 0

(iv) There are total 28 such cards
(26 red cards and 2 black kings).
∴ P (drawn card is a red or a king) = \(\frac{28}{52}=\frac{7}{13}\)

Question 34.
If the median of the distribution given below is 28.5, find the values of x and y.

Class Interval	Frequency
0 – 10	5
10 – 20	x
20 – 30	20
30 – 40	15
40 – 50	y
50 – 60	5
Total	60

Answer:
With the given frequency distribution table, we first prepare a cumulative frequency distribution table as given below:

Class interval	Frequency	Cum. frequency
0 – 10	5	5
10 – 20	x	5 + x
20 – 30	20	25 +x
30 – 40	15	40 + x
40 – 50	y	40 + x + y
50 – 60	5	45 + x + y = 60

Since the median given is 28.5, the median class is 20 – 30.
For this class,
l = 20, h = 10, \(\frac{n}{2}\) = 30, f = 20 and cf = 5 + x.
According to the formula,
Median = l + (\(\frac{\frac{n}{2}-c f}{f}\)) × h
28.5 = 20 + \(\frac{30-(5+x)}{20}\) × 10
⇒ \(\frac{25-x}{2}\) = 8.5
⇒ x = 8
Since, 45 + x + y=60
⇒ 45 + 8 + y = 60
⇒ y = 60 – 53
= 7
Thus, the required values of x and y are 8 and 7 respectively.

Question 35.
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 2 cm and the height of the cone is equal to its radius. Find the volume and surface area of the solid.
Answer:
Given, radius of cone, r ₁ = 2 cm
Height of cone, h ₁ = 2 cm
Radius of hemisphere, r ₂ = 2 cm

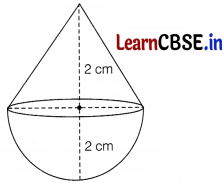
Let V and S be the volume and surface area of the solid.
Then V = volume of cone + Volume of hemisphere
= \(\frac{1}{3}\) πr ₁ ² h ₁ + \(\frac{2}{3}\) πr ₂ ³
= \(\frac{1}{3}\) π [(2) ² × 2 + 2 × (2) ³ ]
= \(\frac{1}{3}\) π (8 + 16)
= \(\frac{24}{3}\) π
= 8π cm ³

and S = Curved surface area of cone + Curved surface area of hemisphere
= πr ₁ l + 2πr ₁ ²
= π (r ₁ l + 2r ₁ ² )
= π (2 + 2 × (2) ² ]
= π (2 × \(\sqrt{2^2+2^2}\) + 8)
= π (2 × 2√2 + 8) ²
= 4π (√2 + 2) cm ²

Section – E
Case study based questions are compulsory

Question 36.
Satellite TV manufacturing businesses tend to have what economists call “economies of scale.” When economies of scale exist, bigness can be its reward.

The more TV’s you manufacture in a single run, lower the costs per unit, which in turn increases your bottom-line margins.

Keeping that in mind, a T.V. manufacturing company increases its production uniformly by fixed number every year. The company produces 8000 sets in the 6 ^th year and 11,300 sets in the 9 ^th year.

Based on the above information, answer the following questions:
(A) Find the company’s production of the first year.
OR
In which year the company’s production is 9100 sets? 2
(B) Find the company’s production of the 8 ^th year. 1
(C) Find the company’s total production of the first 6 years. 1
Answer:
(A) Given a ₆ = 8000
a ₉ = 11,300
Let, the first term be ‘a’ and common difference be ‘d’.
Then, a + (6 – l)d = 8000
⇒ a + 5d = 8,000 ……. (i)
and a + 8d = 11,300 ……. (ii)
On solving (i) and (ii) we get
d = 1,100
⇒ a = 8000 – 5 × 1100
= 2500
OR
Let, the year in which production is 9100 be ‘n’
Then, a _n = a + (n – 1)d
9100 = 2500 + (n – 1) × 1100
⇒ (n – 1) × 1100 = 6600
⇒ n – 1 = 6
⇒ n = 7

(B) Since, a = 2500
and d = 1100
∴ a ₈ = a + (8 – 1)d
= 2500 + 7 × 1100
= 2500 + 7700
= 10,200

(C) Production in 6 ^th year = 8,000
∴ Sn = \(\frac{1}{2}\)[a + l]
= \(\frac{1}{2}\)[2500 + 8000]
= 3 × 10500
= 31,500

Question 37.
Air pollution refers to the release of pollutants into the air that are detrimental to human health and the plant as a whole. In this order Rajasthan government conducted an awareness programme related to environmental localities of a city, the concentration of sulphur dioxide (SO2) in the air (in parts per million i.e. ppm) in 24 are as follows

Concentration of SO 2 (in ppm)	Frequency
0.00 – 0.02	2
0.02 – 0.04	5
0.04 – 0.06	4
0.06 – 0.08	3
0.08 – 0.10	4
0.10 – 0.12	6

Based on the above information, answer the following questions.

(i) Write a formula to find the mean.
Answer:
Mean \((\bar{x})\) = \(\frac{\Sigma f_i x_i}{\Sigma f_i}\)

(ii) Write the formula to find the median.
Answer:
Median = l + \(\left\{\frac{\frac{N}{2}-c f}{f}\right\}\) × h

(iii) Find the mean concentration of SO ₂ .
Answer:
the table for the given distribution is,

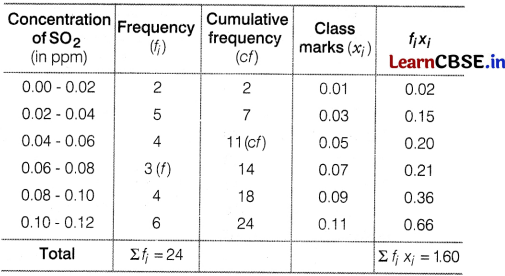
Here, Σf _i x _i = 1.60
and Σf _i = 24
∴ Mean of concentration of SO ₂ = \(\frac{\Sigma f_i x_i}{\Sigma f_i}\)
= \(\frac{1.60}{24}\)
= 0.066 (approx)

Or
Find the median concentration of SO ₂ .
Answer:
Here, N = 24
⇒ \(\frac{N}{2}\) = 12
The cumulative frequency just greater than 12 is 14
and the corresponding class interval is 0.06 – 0.08.
Here, l = 0.06,
cf = 11,
f = 3
and h = 0.02
∴ Median = l + \(\left\{\frac{\frac{N}{2}-c f}{f}\right\}\) × h
= 0.06 + \(\left\{\frac{\frac{24}{2}-11}{3}\right\}\) × 0.02
= 0.06 + \(\left\{\frac{12-11}{3}\right\}\) × 0.02
= 0.06 + \(\frac{0.02}{3}\)
= 0.06 + 0.006
= 0.066 (approx.)

Question 38.
All of them know that smoking is injurious to health. So, college students decide to make a campaign.
To raise social awareness about the hazards of smoking, a school decided to start a “No SMOKING” campaign. 10 students are asked to prepare campaign banners in the shape of triangles (as shown in the figure)

Based on the above information, answer the following questions:
(A) If the cost per square centimetre of banner is ₹2, then find the overall cost incurred on such campaign.
OR
If we want to draw a circumscribed circle of given, then find the coordinate of the centre of circle. 2
(B) If we draw the image of figure about the line BC, then find the total area. 1
(C) Find the centroid of the given triangle. 1
Answer:
(A) Here from the figure,
Coordinates of A = (1, 1).
Coordinates of B = (6,1)
and Coordinates of C = (1, 5)
∴ Area of banner = Area of ΔABC
Now, area of one banner
\(\frac{1}{2}\) × AB × AC
\(\frac{1}{2}\) × 5 × 4 = 10

Then, area of 10 banners = 10 × Area of one banner
∴ Cost of 10 banners at the rate of ₹ 2 per cm ²
= 2 × Area of 10 banners
= 2 × 10 × 10
= ₹ 200
OR
The center of the circumscribed circle of a given triangle is the mid-point of the hypotenuse.
Centre of circle = Mid-point of BC
= (\(\frac{1+6}{2}, \frac{5+1}{2}\))
= (\(\frac{7}{2}, \frac{6}{2}\))
= (3.5, 3)

(B) Total area of the required figure
= 2 × Area of ΔABC
= 2 × 10 = 20

(C) The centroid of the given triangle
= (\(\frac{1+1+6}{3}, \frac{5+1+1}{3}\))
= (\(\frac{8}{3}, \frac{7}{3}\))