CBSE Sample Papers for Class 10 Maths Basic Set 2 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Basic with Solutions Set 2 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Basic Set 2 with Solutions

Time : 3 hrs
Max. Marks : 80

General Instructions:

1. This Question Paper has 5 Sections A, B, C, D and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answer-I (SA-I) type questions carrying 2 marks each.
4. Section C has 6 Short Answer-II (SA-II) type questions carrying 3 marks each.
5. Section D has 4 Long Answer (LA) type questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment questions (4 marks each).
7. All Questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks and 2 Questions of 5 marks has been provided. An internal choice has been provided in the 2 marks question of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section – A
Section A consists of 20 questions of 1 mark each

Question 1.
which of the following equation has root as 3?
(a) x ² – 5x + 6 = 0
(b) – x ² + 3x – 3 = 0
(c) √2 x ² – \(\frac{3}{\sqrt{2}}\) x + 1 = 0
(d) 3x ² – 3x + 3 = 0
Answer:
(a) x ² – 5x + 6 = 0

Given that x ² – 5x + 6 = 0
On putting x = 3, we get
(3) ² – 5 (3) + 6 = 9 – 15 + 6 = 0
Hence, x = 3 is a root of the equation.
From option (b),
– x2 + 3x – 3 = 0
On putting x = 3, we get
– (3) ² + 3 (3) – 3 = – 9 + 9 – 3
= – 3 ≠ 0
Hence, x = 3 is not a root of the equation.
From option (c),
√2 x ² – \(\frac{3}{\sqrt{2}}\) x + 1 = 0
On putting x = 3, we get
√2 (3) ² – \(\frac{3(3)}{\sqrt{2}}\) + 1
9√2 – \(\frac{9}{\sqrt{2}}\) + 1 ≠ 0
Hence, x = 3 is not a root of the equation.
From option (d),
3x ² – 3x + 3 = 0
On putting x = 3, we get
3 (3) ² – 3 (3) + 3 = 37 – 9 + 3
= 21 ≠ 0
Hence, x = 3 is not a root of the equation.

Question 2.
If p, 2p – 1, 2p + 1 are three consecutive terms of an A.P., then the value of ‘p’ is: 1
(a) 3
(b) 4
(c) 5
(d) 6
Answer:
(a) 3
Explanation: Since p, 2p – 1 and 2p + 1 are three consecutive terms of an A.P.,
2(2p – 1) = p + (2p + 1)
⇒ 4p – 2 = 3p + 1
⇒ P = 3

Question 3.
If a number x is added to twice its square, then the resultant is 21. Then, the quadratic representation of this statement is
(a) 2x ² – 2 + 21 = 0
(b) 2x ² + x – 21 = 0
(c) 2x ² – x – 20 = 0
(d) None of these
Answer:
(b) 2x ² + x – 21 = 0

Let the number be x.
Then, according to the given condition,
2x ² + x = 21
⇒ 2x ² + x – 21 = 0

Question 4.
If the radii of two concentric circles are 4 cm and 5 cm, then the length of the chord to one circle which is tangent to the other circle is: 1
(a) 6 cm
(b) 5 cm
(c) 8 cm
(d) 9 cm
Answer:
(a) 6 cm
Explanation:

We know tangent is perpendicular to radius at the point of contact.
∴ OP ⊥ AB
Also, AB is a chord to outer circle and perpendicular from centre to the chord bisects it.
∴ AP = BP = \(\frac{1}{2}\) AB
In right ΔOPA,
AP = \(\sqrt{O A^2-O P^2}\)
= \(\sqrt{5^2-4^2}\)
= \(\sqrt{25-16}\)
= √9
= 3 cm
Thus, AB = 2 × AP
= 6 cm

Question 5.
If the lines given by 2x + ky = l and 3x – 5y = 7 have unique solutions, then the value of k is
(a) – \(\frac{10}{3}\)
(b) All real values
(c) \(\frac{10}{3}\)
(d) All real values, except
Answer:
(d) All real values, except

(d) The given equations can be rewritten as,
2x + ky – 1 = 0 and 3x – 5y – 7 = 0
On comparing with a ₁ x + b ₁ y + c ₁ = 0
and a ₂ x + b ₂ y + c ₂ = 0,
we get a ₁ = 2, b ₁ =/r, c ₁ = – 1
and a ₂ = 3, b ₂ = – 5, c ₂ = – 7
For unique solution,
\(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
⇒ \(\frac{2}{3} \neq \frac{k}{-5}\)
⇒ k ≠ – \(\frac{10}{3}\)
Thus, the given lines have a unique solution for all real values of k, except – \(\frac{10}{3}\).

Question 6.
In the given figure, D and E are two points lying on side AB, such that AD = BE. If DP || BC and EQ||AC then: 1

(a) PQ || AB
(b) PQ = AB
(c) PQ || CD
(d) PQ = AC
Answer:
(a) PQ || AB
Explanation: In ΔABC, we have DP || BC and EQ || AC
∴ By BPT theorem,
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AP}}{\mathrm{PC}}\)
and \(\frac{B E}{E A}=\frac{B Q}{Q C}\)
⇒ \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{BQ}}{\mathrm{QC}}\)
[∵ EA = ED + DA = ED + BE = BD]
⇒ \(\frac{\mathrm{AP}}{\mathrm{PC}}=\frac{\mathrm{BQ}}{\mathrm{QC}}\)
∴ PQ || AB [By converse of BPT theorem]

Question 7.
The distance of the point (12, 5) from the origin is
(a) 25 units
(b) 13 units
(c) \(\sqrt{13}\) units
(d) \(\sqrt{35}\) units
Answer:
(b) 13 units

Let the point be P(12, 5) and origin (0, 0).
Distance between two points = \(\sqrt{(0-12)^2+(0-5)^2}\)
= \(\sqrt{144+25}\)
= \(\sqrt{169}\)
= 13 units

Question 8.
In the distribution given below, the frequency of the class succeeding the modal class is: 1

Marks	Frequency
Below 10	3
Below 20	12
Below 30	27
Below 40	57
Below 50	75
Below 60	80

(a) 15
(b) 5
(c) 9
(d) 18
Answer:
(d) 18
Explanation:

Marks	Frequency
0 – 10	3
10 – 20	9
20 – 30	15
30 – 40	30
40 – 50	18
50 – 60	5

Here, maximum frequency is 30, which belongs to class 30 – 40. So, the modal class is 30 – 40.
The class succeeding the modal class is 40 – 50 with frequency 18.

Question 9.
If 2 is a zero of polynomial p(x) = 4x ² + 2x – 5a, then the value of a is
(a) – \(\frac{5}{2}\)
(b) 4
(c) 2
(d) 6
Answer:
(b) 4

Given polynomial is p(x) = 4x ² + 2x – 5a
Since, 2 is a zero of polynomial.
∴ P(2) = 0
⇒ 4(2) ² + 2(2) – 5a = 0
⇒ 16 + 4 – 5a = 0
⇒ 5a = 20
⇒ a = 4

Question 10.
In the given figure, x is: 1

(a) \(\frac{a b}{a+b}\)
(b) \(\frac{a c}{b+c}\)
(c) \(\frac{b c}{b+c}\)
(d) \(\frac{a c}{a+c}\)
Answer:
(b) \(\frac{a c}{b+c}\)
Explanation: In ΔKPN and ΔKLM,
∠K is common and we have
∠KNP = ∠KML = 46
Thus by A – A criterion of similarity
ΔKNP ~ ΔKML
Thus \(\frac{\mathrm{KN}}{\mathrm{KM}}=\frac{\mathrm{NP}}{\mathrm{ML}}\)
\(\frac{c}{b+c}=\frac{x}{a}\)
x = \(\frac{a c}{b+c}\)

Question 11.
The radius of the wheel of a bus is 20cm. If the speed of the bus is 30 km/h, then how many revolutions will the wheel make in 1 mm?
(a) 390
(b) 398
(c) 326
(d) 450
Answer:
(b) 398

In 1 h, distance covered by wheel = 30 km
In 1 mm, distance covered by wheel = \(\frac{30 \times 1000}{60}\) = 500 m
Number of revolutions made in 1 min = Distance covered by wheel / Circumference of the wheel
= \(\frac{500}{2 \times \frac{22}{7} \times \frac{20}{100}}\)
= \(\frac{500 \times 7 \times 100}{2 \times 22 \times 20}\)
= \(\frac{50 \times 25 \times 7}{22}\)
= \(\frac{625 \times 7}{11}\)
= 398 (approx)

Question 12.
In figure XY ||QR and \(\frac{P X}{X Q}=\frac{P Y}{Y R}=\frac{1}{2}\), then the value of XY is: 1

(a) \(\frac{1}{3}\)QR
(b) \(\frac{1}{3}\)XQ
(c) \(\frac{1}{3}\)PQ
(d) \(\frac{1}{3}\)PR
Answer:
(a) \(\frac{1}{3}\)QR
Explanation:

Question 13.
The midpoint of the line segment joining the points (- 7, 9) and (- 3, 5) is
(a) \(\left(\frac{5}{2}, \frac{7}{2}\right)\)
(b) (2, 7)
(c) (- 5, 7)
(d) (5, 2)
Answer:
(c) (- 5, 7)

Given, (x ₁ , y ₁ ) = (- 7, 9) and (x ₂ , y ₂ ) = (- 3, 5)
Let the mid point be (x, y).
∴ x = \(\frac{x_1+x_2}{2}\)
= \(\frac{-7-3}{2}=\frac{-10}{2}\)
= – 5
and y = \(\frac{y_1+y_2}{2}\)
= \(\frac{9+5}{2}=\frac{14}{2}\) = 7
∴ Mid-point is (- 5, 7).

Question 14.
The ratio of the length of a rod and its shadow is √3 : 1. Then, the angle of elevation of the Sun, is
(a) 45°
(b) 40°
(e) 30°
(d) 60°
Answer:
(d) 60°

Let the length of rod be BC and length of shadow be AB.

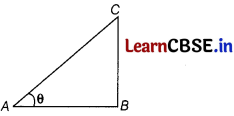
Then, \(\frac{B C}{A B}=\frac{\sqrt{3}}{1}\) [given]
Let θ be the angle of elevation of Sun.
Then, tan θ = \(\frac{B C}{A B}=\frac{\sqrt{3}}{1}\)
θ = 60°

Question 15.
In an arithmetic progression, if a = 6, d = – 8 and n = 6 then a _n is
(a) – 17
(b) – 30
(c) – 34
(d) Cannot be determined
Answer:
(c) – 34

Given, a = 6,
d = – 8
and n = 6
a _n = a + (n – 1) d
= 6 + ( 6 – 1) × (- 8)
= 6 + 5 × (- 8)
= 6 – 40
= – 34

Question 16.
The ratio of LCM and HCF of the least composite and the least prime numbers is: 1
(a) 1 : 2
(b) 2 : 1
(c) 1 : 1
(d) 1 : 3
Answer:
(b) 2 : 1
Explanation: Least composite number is 4 and the least prime number is 2.
LCM (4, 2): HCF (4, 2) = 4 : 2 = 2 : 1

Question 17.
If the probability of Sania winning a tennis match is 0.63, then the probability of her losing the match is
(a) 0.63
(b) 1
(c) 0
(d) 0.37
Answer:
(d) 0.37

Let E be the event Sania winning the match, then
P(E) = 0.63 [given]
∴ P (Sania losing the match) = P(not E)
= P(\((\bar{E}\))
= 1 – P (E)
= 1 – 0.63
= 0.37

Question 18.
In the given figure, ΔABC ~ ΔPQR. The value of x is: 1

(a) 4 cm
(b) 6 cm
(c) 3 cm
(d) 5 cm
Answer:
(c) 3 cm
Explanation: Since, ΔABC ~ ΔPQR
Then, \(\frac{A B}{P Q}=\frac{B C}{R Q}=\frac{A C}{P R}\)
⇒ \(\frac{6}{4.5}=\frac{4}{x}=\frac{5}{3.75}\)
⇒ x = \(\frac{4 \times 4.5}{6}\)
= 3 cm

Directions: In question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.

Question 19.
Assertion (A) : Three consecutive terms k, 2k + 1, 5k – 2 form an AP, then k is equal to 2.
Reason (R) : In an AP : a, a + d, a + 2d ……….., the sum of n terms of AP is
S _n = \(\frac{n}{2}\) [a + (n – 1) d]
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(c) Assertion (A) is true but Reason (R) is false.

Taking first two terms,
Common difference = 2k + 1 – k = k + 1
Taking second and third terms,
Common difference = 5k – 2 – 2k – 1 = 3k – 3
Since, the terms are in AP
∴ k + 1 = 3k – 3
⇒ – 2k = – 4
⇒ k = 2
So, the given Assertion (A) is true.
We know that sum of n terms of an AP
= \(\frac{n}{2}\) [2a + (n – 1) d] ≠ \(\frac{n}{2}\) [a + (n – 1)d]
So, the given Reason (R) is false.

Question 20.
Assertion (A): 2x ² – 4x + 3 = 0 is a quadratic equation.
Reason (R): All polynomials of degree n, when n is a whole number can be treated as quadratic equation. 1
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Answer:
(c) Assertion (A) is true but reason (R) is false.
Explanation: Assertion (A) is true but Reason (R) is false as only polynomials of degree 2, can be treated as quadratic equations.

Section B
Section B consists of 5 questions of 2 marks each

Question 21.
Find the radius of a circle, if the length of tangent from a point at distance of 13 cm from the centre of the circle is 12 cm.
Answer:
Let AB be a tangent drawn from point B to a circle with centre 0 such that AB = 12 cm and OB = 13 cm.
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ In ∆AOB, OA ⊥ AB

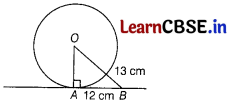
Now, in right angled ∆ OAB,

OB ² = OA ² + AB ²
⇒ (13) ² = OA ² + (12) ²
⇒ 169 = OA ² + 144
⇒ OA ² = 169 – 144 = 25
⇒ OA = 5 cm
Hence, the radius of the required circle is 5 cm.

Question 22.
Evaluate: (sin ⁴ 60° + sec ⁴ 30°) – 2 (cos ² 45° – sin ² 90°)
OR
Prove that \(\frac{\sin \theta-2 \sin ^3 \theta}{2 \cos ^3 \theta-\cos \theta}\) = tan θ 2
Answer:
(sin ⁴ 60° + sec ⁴ 30°) – 2(cos ² 45° – sin ² 90°)

OR
L.H.S = \(\frac{\sin \theta-2 \sin ^3 \theta}{2 \cos ^3 \theta-\cos \theta}\)

Question 23.
A teacher told his student to write a quadratic polynomial whose sum and product of the zeroes are – 6 and 8, then the students write the polynomial x ² + 6x + 8. Is it right? Justify your answer.
Answer:
Yes, we know that, if α and β are the zeroes of quadratic polynomial, then the quadratic polynomial
= x ² – (Sum of zeroes) x + Product of zeroes
∵ Required polynomial = x ² – (- 6) x + 8
= x ² + 6x + 8.

Question 24.
Find a point on x-axis which is equidistant from A (-3, 4) and B (7, 6). 2
Answer:
Let P (x, 0) be a point on x-axis, equidistant from A (-3, 4) and B (7, 6), i.e.,
AP = BP or AP ² = BP ²
i.e. (- 3 – x) ² + (4 – 0) ² = (7 – x) ² + (6 – 0) ²
i.e. 9 + x2 + 6x + 16 = 49 + x ² – 14x + 36
⇒ 6x + 25 = – 14x + 85
⇒ 20x = 60
⇒ x = 3
Thus, the required point is (3, 0).

Question 25.
Prove that tan ² θ + cot ² θ + 2 = sec ² θ cosec ² θ

Answer:
LHS = tan ² θ + cot ² θ + 2
= (1 + tan ² θ) + (1 + cot ² θ)
= sec ² θ + cosec ² θ (1)
= \(\frac{1}{\cos ^2 \theta}+\frac{1}{\sin ^2 \theta}\)
= \(\frac{\sin ^2 \theta+\cos ^2 \theta}{\cos ^2 \theta \sin ^2 \theta}\)
= \(\frac{1}{\cos ^2 \theta \sin ^2 \theta}\)
= \(\frac{1}{\cos ^2 \theta} \cdot \frac{1}{\sin ^2 \theta}\)
= sec ² θ cosec ² θ
= RHS
Hence proved.

Or

Prove that (cosec A – sin A) (sec A – cos A) = sin A cos A
Solution:
LHS = (cosec A – sin A) (sec A – cos A)
= \(\left(\frac{1}{\sin A}-\sin A\right)\left(\frac{1}{\cos A}-\cos A\right)\)
= \(\frac{1-\sin ^2 A}{\sin A} \times \frac{1-\cos ^2 A}{\cos A}\)
= \(\frac{\cos ^2 A}{\sin A} \times \frac{\sin ^2 A}{\cos A}\)
= cos A sin A
= RHS
Hence proved.

Section C
Section C consists of 6 questions of 3 marks each

Question 26.
The sum of the squares of two consecutive multiples of 7 is 637. Find the two multiples.
OR
The length and breadth of a rectangle are (3x + 1) cm and (2x – 1) cm respectively. If the area of the rectangle is 144 sq. cm, then find the value of x. 3
Answer:
Let 7x and 7(x + 1) be two consecutive multiples of 7.
Then,
(7x) ² + [7 (x + 1)] ² = 637
⇒ 49x ² + 49 (x ² + 2x + 1) = 637
⇒ 98x ² + 98x + 49 = 637
⇒ 98x ² + 98x – 588 = 0
⇒ x ² + x – 6 = 0
⇒ (x + 3)(x – 2) = 0
⇒ x + 3 = 0 or x – 2 = 0
⇒ x = -3 or x = 2
Thus, two consecutive multiples of 7 are 14 and 21, or – 21 and – 14.
OR.
Given, length of a rectangle = (3x + 1) cm
Breadth of a rectangle = (2x – 1) cm
Area of a rectangle = 144 sq. cm
ATQ,
Area of rectangle = l × b
⇒ (3x + 1) (2x – 1) = 144
⇒ 6x ² + 2x – 3x – 1 = 144
⇒ 6x ² – x – 1 = 144
6x ² – x – 145 = 0
Solving by using quadratic formula,

Question 27.
Find the largest positive integer that will divide 444, 486 and 604 leaving remainders 7, 11 and 15, respectively.
Solution:
It is given that on dividing 444 by the required number, there is a remainder of 7.
This means that 444 – 7 = 437 is exactly divisible by the required number.
In other words, required number is a factor of 437.
Similarly, required positive integer is a factor of
486 – 11 = 475
and 604 – 15 = 589.
Required number is the HCF of 437, 475 and 589.
Using the factor tree method, the prime factorisations of 437, 475 and 589 are as follows
437 = 19 × 23
475 = 5 ² × 19
and 589 = 19 × 31
Hence, required number = 19.

Question 28.
Prove that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at the centre.
OR
In the given figure, PT is a tangent and PAB is a secant. If PT = 6 cm and AB = 5 cm then find the length of PA. 3

Answer:
Let, AB and CD are two tangents to a circle and AB || CD. Tangent BD subtends ∠BOD at ‘the centre.
To prove: ∠BOD = 90°
Construction: Join OP, OQ and OR.

Proof: Here, OP ⊥ BD
[∵ tangent at any point of a circLe is perpendicular to the radius through the point of contact]
In right anged ΔOQB and ΔOPB.
BQ = BP
[∵ the lengths of tangents drawn from an external point are equal]
OQ = OP [radii]
OB = OB [common]
∴ ΔOQB = ΔOPB [b SSS congruency]
Then ∠1 = ∠2 [by CPCT] …….. (i)
Similarly, in right angled ΔOPD and ΔORD,
∠3 = ∠4 …….. (ii)
∴ ∠BOD = ∠1 + ∠3
= \(\frac{1}{2}\)(2∠1 + 2∠3)
= \(\frac{1}{2}\)(∠1 + ∠1 + ∠3 + ∠3)
= \(\frac{1}{2}\)(∠1 + ∠2 + ∠3 + ∠4)
[from Eqs. (i) and (ii)]
= \(\frac{1}{2}\)(180°) = 90°
[∵ QR is a straight line, therefore ∠1 + ∠2 + ∠3 + ∠4 = 180°]
Hence, proved.
OR
Given, PT and PAB be a tangent and a secant, respectively of a circle.
Also, PT = 6 cm and AB = 5 cm Join OT, OA and OP. Draw OC ⊥ AB.
Let radius of circle be r

∴ OT ⊥ PT
[∵ tangent is perpendicular to the radius at the point of contact]
In right angled ΔOTP,
(OP) ² = (PT) ² + (OT) ²
[by Pythagoras theorem]
⇒ (OP) ² = 6 ² + r ²
⇒ (OP) ² – r ² = 36
⇒ (OP) ² – (OA) ² = 36 [∵ OA = OT = r] …….. (i)
Also, in right angled ΔOCA
(OA) ² = (OC) ² + (AC) ²
[by Pythagoras theorem]
On putting the value of OA ² in Eq. (i), we get
(OP) ² – (OC ² + AC ² ) = 36
⇒ (OP) ² – (OC) ² – (AC) ² = 36
⇒ (PC) ² – (AC) ² = 36 [∵ In ΔOCP, (OP) ² – (OC) ² = (PC) ² ]
⇒ (PC – AC)(PC + AC) = 36 [a ² – b ² = (a – b)(a + b)]
⇒ AP (PC + BC) = 36
⇒ AP(PB) = 36
⇒ AP(AP + AB) = 36
⇒ AP(AP + 5) = 36 [∵ AB = 5 cm]
⇒ AP ² + 5AP -36 = 0
⇒ (AP + 9)(AP – 4) = 0
⇒ AP = 4 or – 9
Hense AP = 4 cm [∵ side cannot be negative]

Question 29.
A Rafree is standing on the side of the athletic track and kept a stopwatch, which is used to find the time that it took a group of students to run 200 m.

In different time intervals, different number of students completed the race are given in the table as shown below

Find mode of the given data.
Answer:
The highest frequency in the given data is 15 whose modal class is 50-100.
Here, l = 50,
f = 15,
f ₁ = 10,
f ₂ = 7
and h = 50
∵ Mode = l + \(\frac{f-f_1}{2 f-f_1-f_2}\) × h
= 50 + \(\frac{15-10}{2 \times 15-10-7}\) × 50
= 50 + \(\frac{5 \times 50}{30-17}\)
= 50 + \(\frac{250}{13}\)
= 50 + 19.23
= 69.23

Question 30.
If a + b = c + d where a, b, c, d are rational numbers, then prove that either a = c and b = d or b and d are squares of rational numbers. 3
Answer:
Let a = c, then
a + √b = c + √d
⇒ √b = √d
⇒ b = d
So let a ≠ c, then, there exist a positive rational number x, such that a = c + x.
Now, a + √b = c + √d
⇒ c + x + √b = c + √d [∵ a = c+ x]
⇒ x + √b = √d ………. (i)
Squaring on both site, we get
⇒ (x + √b) ² = (√d) ²
⇒ x + 2√b x + b = d
⇒ √b = \(\frac{d-x^2-b}{2 x}\)
⇒ √b is rational [∵ d, x, b are rationals, … \(\frac{d-x^2-b}{2 x}\) is rational]
⇒ b is a square of a rational number From (i), we have
√d = x + √b
⇒ √d is rational
⇒ d is the square of a rational number
Hence, either a = c and b = d or b and d are the squares of rational numbers.

Question 31.
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Answer:
We have, an ∆ABC in which AB = BC = CA and AD ⊥ BC

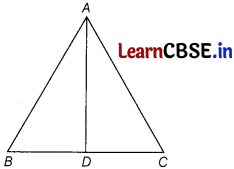
To prove 3AB ² = 4AD ²
Proof In ∆ADB and ∆ADC,
we have
AB = AC [given]
∠B = ∠C = 60°
and ∠ADB = ∠ADC = 90°
∆ADB = ∆ADC [MS congruence rule]
BD = DC = \(\frac{1}{2}\) BC
From right angled ∆ADB, we have
AB ² = AD ² + BD ² [by Pythagoras theorem]
= AD ² + (\(\frac{1}{2}\) BC) ²
= AD ² + \(\frac{1}{4}\) BC ²
⇒ 4AB ² = 4AD ² + BC ²
⇒ 3AB ² = 4AD ² [∵ BC = AB]
⇒ 3AB ² = 4AD ²

Section D
Section D consists of 4 questions of 5 marks each

Question 32.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined:
(A) \(\frac{\tan \theta}{1-\cot \theta}+\frac{\cot \theta}{1-\tan \theta}\) = 1 + sec θ cosec θ
(B) (sin A + cosec A) ² + (cos A + sec A) ²
= 7 + tan ² A + cot ² A 5
Answer:



= 5 + cosec ² A + sec ² A
= 5 + 1 + cot ² A + 1 + tan ² A
[∵ cosec ² θ = 1 + cot ² θ, sec ² θ = 1 + tan ² θ]
= 7 + tan ² A + cot ² A
= R.H.S.

Question 33.
ABC is an isosceles triangle with AB = AC and D is a point on AC such that BC ² = AC × DC, then prove that BD = BC.
Answer:
We have, BC ² = AC × DC
⇒ BC × BC = AC × DC
⇒ \(\frac{B C}{D C}=\frac{A C}{B C}\)
In ∆ABC and ∆BDC,
\(\frac{B C}{D C}=\frac{A C}{B C}\)
and ∠C = ∠C [common]

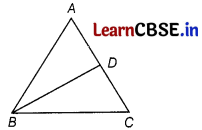
∴ ∆ABC ~ ∆BDC
[by SAS similarity critetian] (1)
⇒ \(\frac{A C}{B C}=\frac{A B}{B D}\)
⇒ \(\frac{A C}{B C}=\frac{A C}{B D}\)
[∵ AB = AC]
⇒ BD = BC
Hence proved.

Question 34.
In one corner of the drawing room, a flower basket is kept inside the glass, lies on the table. The basket is designed in such a way that every one pleases to see it.
The shape of flower basket is hemisphere with ratio 60 cm and upper shape is conical with height 120 cm from the bottom surface.

(A) Find the capacity of the glass.
(B) Find the volume of the cone. 5
Answer:
(A) Height of the cylinder, h = 180 cm = 1.8 m [∵ 1 cm = \(\frac{1}{100}\)m]
Radius of the cylinder, r = 60 cm = 0.6 m
∴ Capacity of glass = Volume of cylinder
= πr ² h
= \(\frac{22}{7}\) × 0.6 × 0.6 × 1.8
= \(\frac{14.256}{7}\)m ³

(B) Height and radius of cone are
h ₁ = 120 cm = 1.2 m
r ₁ = 60 cm = 0.6 m
Volume of cone = \(\frac{1}{3}\)πr ₁ ² 2h ₁
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × (0.6) ² × (1.2)
= \(\frac{22}{21}\) × 0.432
= 0.45 m ³

Question 35.
A straight highway leads to the foot of a national communication and telecasting tower. A watchman standing at the top of the tower observes a car at an angle of
depression of 30° which is approaching the foot of the tower with a uniform speed. Two minutes later, the angle of depression was found to be 60°.

Find the time taken by the car to reach the foot of the tower from this point. The watchman suspects that some terrorist are approaching the tower. It needs half a minute for the watchman to inform the security staff to be on the alert.
Answer:
Let AB be the tower of height h m, C and D be the position of car at an angle of depression of 30° and 60°, respectively.
Also, let the speed of car be x km/min and y min will be taken by the car to cover distance BD.

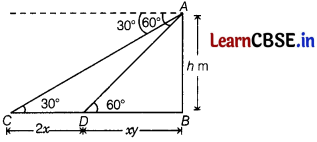
Then, CD = 2x km
[∵ time taken to cover distance CD is 2 min and
Distance = Speed × Time]
and BD = xy km
Now, in ∆ABC, we have
tan 30° = \(\frac{A B}{B C}\)
[∵ tan θ = \(\frac{\text { Perpendicular }}{\text { Base }}\)]
\(\frac{1}{\sqrt{3}}=\frac{A B}{B D+C D}\)
[∵ tan 30° = \(\frac{1}{\sqrt{3}}\)]
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{2 x+x y}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{x(2+y)}\) …………..(i)
and in ∆ABD, we have
tan 60° = \(\frac{A B}{B D}\)
⇒ √3 = \(\frac{h}{x y}\)
⇒ \(\frac{h}{x}\) = √3 y
[∵ tan 60° = √3]
On substituting the value of \(\frac{h}{x}\) in Eq. (i), we get
\(\frac{1}{\sqrt{3}}=\frac{\sqrt{3} y}{2+y}\)
⇒ 2 + y = 3y
⇒ 2 = 2y
⇒ y = 1
Hence, my car will take 1 min to reach the toot of the tower.

Section – E
Case study based questions are compulsory

Question 36.

Mr. Naik is a paramilitary Intelligence Corps officer who is tasked with planning a coup on the enemy at a certain date. Currently 1 he is inspecting the area standing on top of the cliff. Agent Vinod is on a hot air balloon, in the sky. When Mr. Naik looks down below the cliff towards the sea, he has Ajay and Maran in boats positioned to get a good vantage point.

The main goal is to scope out the range and angles at which they should train their soldiers.

Based on the above information, answer the following questions:
(A) Write a pair of‘angle of elevation’ and ‘angle of depression’. 1
(B) If the vertical height of the balloon from the top of the cliff is 12 m and ∠b = 30°, then find the distance between the Naik and Vinod. 1
(C) Ajay’s boat is 25 m away from the base of the cliff. If ∠d = 30°. What is the height of the cliff?
(Use √3 = 1.73).
OR
If the height of the cliff is 30 m, ∠c = 45° and ∠d = 30°, then find the horizontal distance between the two
boats (use √3 = 1.73). 2
Answer:
(A) A pair of ‘angle of elevation’ is ∠b°, ∠e° and one pair of angle of depression is ∠c° and ∠d°

(B) Then, sin 30°
= \(\frac{\text { Vertical height }}{\text { Distance between Naik and Vinod }}\)
⇒ \(\frac{1}{2}=\frac{12}{D_{\text {Nand } V}}\)
⇒ Distance = 24 m

(C) Here, ∠d° = ∠f° = 30°


And ∠d = ∠f = 30°
∴ tan 30° = \(\frac{\text { height of cliff }}{\text { Distance of Ajay’s boat }}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{30}{D_A}\)
⇒ D _A = 3√3
∴ Distance between boats
= 30√3 – 30
= 30(√3 – 1)
= 30(1.73 – 1)
= 30 × 0.73
= 21.9 m

Question 37.
A regular morning walk, schedule can help you to reduce weight. You can take care of many health problems concerning your heart, joints, mental health, lung capacity, immune system and body strength just by walking. To improve the health two friends Vicky and Love went to the walk on concrete track. (Shown in figure). In the figure, AOB is a flower bed in the shape of a sector of a circle of radius 40 m and ∠AOB = 60°. Also, a 15 m wide concrete track is made as shown in the figure.

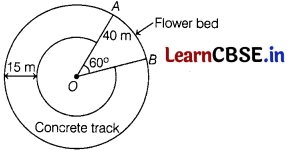
On the basis of above information, answer the following questions.

(i) Find the radius of inner circle. (1)
Answer:
Let radius of inner circle be r ₂ and outer circle be r ₁
and given concrete track width = 15 m
∵ r ₁ = 40 [given]
∵ r ₂ = r ₁ – 15
= 40 – 15 = 25 m

(ii) Write the formula to find the area of sector. (1)
Answer:
Area of sector = \(\frac{\theta}{360^{\circ}}\) × πr²

(iii) Find the area of the sector AOB. (2)
Answer:
Area of sector AOB = \(\frac{60^{\circ}}{360^{\circ}} \times \frac{22}{7}\) × 40 × 40
= \(\frac{1}{6} \times \frac{22}{7}\) × 40 × 40
= 838.09 m ²

Or

If instead of flower bed there had been a complete circular concrete track, then find the area of the concrete region. (2)
Answer:
∴ Required area = Area of complete circle -Area of inner circle = π × (40) ² – π × (25) ²
= π (40 ² – 25 ² )
= π (40 + 25) (40 – 25)
= 65 × 15 × π
= 975 π m ²

Question 38.
While playing in the garden, Sahiba saw a honeycomb and asked her mother what is that. She replied that it’s a honeycomb made by honey bees to store honey. Also, she told her that the shape of the honeycomb formed is parabolic. The mathematical representation of the honeycomb structure is shown in the graph.

Based on the above information, answer the following questions:
(A) What will be the expression of the polynomial represented by the graph? 1
(B) Find the value of the polynomial represented by the graph when x = 6 and – 6. 1
(C) Find the sum of zeroes of the obtained polynomial in question (A). Also, find the value of the expression at x = 5.
OR
If the sum of zeroes of polynomial at ² + 5t + 3a is equal to their product, then find the value of a. Also find the values of the expression at t = – 3. 2
Answer:
(A) Since the graph of the polynomial cuts the x-axis at (- 6, 0) and (6,0). So, the zeroes of polynomials are – 6 and 6.
∴ Required polynomial is
p(x) = x ² – (- 6 + 6)x + (- 6)(6)
= x ² – 36

(B) From the graph, it is clear that P(6) = 0 and P(- 6) = 0.

(C) Let P(x) = x ² – 36. Then, the coefficient of x
Sum of zeroes = \(\frac{\text { coefficient of } x}{\text { coefficient of } x^2}\)
= – \(\frac{0}{1}\) = 0
P(5) = 5 ² – 36 = -11
OR
The given polynomial is at ² + 5t + 3a
Given, the sum of zeroes = product of zeroes
⇒ \(\frac{-5}{a}=\frac{3 a}{a}\)
⇒ a = \(\frac{-5}{3}\)
At t = – 3,
(\(\frac{-5}{3}\))(-3) ² + 5(-3) + 3(\(\frac{-5}{3}\)) = -35