CBSE Sample Papers for Class 10 Maths Basic Set 1 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Basic with Solutions Set 1 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Basic Set 1 with Solutions

Time : 3 hrs
Max. Marks : 80

General Instructions:

1. This Question Paper has 5 Sections A, B, C, D and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answer-I (SA-I) type questions carrying 2 marks each.
4. Section C has 6 Short Answer-II (SA-II) type questions carrying 3 marks each.
5. Section D has 4 Long Answer (LA) type questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment questions (4 marks each).
7. All Questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks and 2 Questions of 5 marks has been provided. An internal choice has been provided in the 2 marks question of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section – A
Section A consists of 20 Questions of 1 mark each

Question 1.
If two positive integers a and b are written as a = x ³ y ² and b = xy ³ where x and y are prime numbers, then HCF (a, b) is
(a) xy
(b) xy ²
(c) x ³ y ³
(d) x ² y ²
Answer:
(b) xy ²

Here, a = x ³ y ² = xy ² (x ² )
and b = xy ³
= xy ² (y)
∴ HCF (a, b) = xy ²

Question 2.
The LCM of smallest two-digit composite number and smallest composite number is: 1
(a) 12
(b) 4
(c) 20
(d) 44
Answer:
(c) 20
Explanation: As we know, the smallest two digit composite number is 10 and the smallest composite number is 4.
By prime factorisation, we get
4 = 1 × 2 × 2
10 = 1 × 2 × 5
Now, LCM of (4, 10) = 2 × 2 × 5 = 20

Question 3.
If x = 3 is one of the roots of the quadratic equation x ² – 2kx – 6 = 0, then the value of k is
(a) – \(\frac{1}{2}\)
(b) \(\frac{1}{2}\)
(c) 3
(d) 2
Answer:
(b) \(\frac{1}{2}\)

Given quadratic equation is x ² – 2kx – 6 = 0
∵ x = 3 is a root of the equation.
(3) ² – 2k (3) – 6 = 0
⇒ 9 – 6k – 6 = 0
⇒ 3 = 6k
⇒ k = \(\frac{1}{2}\)

Question 4.
The pair of equations y = 0 and y = -7 has: 1
(a) one solution
(b) two solution
(c) infinitely many solutions
(d) no solution
Answer:
(d) no solution
Explanation: Given, the pair of equations are y = 0 and y = -7.
Hence b ₁ = 1, c ₁ = 0
b ₂ = 1, c ₂ = 7
So \(\frac{b_1}{b_2}=\frac{1}{1}\) = 1
So \(\frac{c_1}{c_2}=\frac{0}{-7}\) = 0
∴ \(\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Therefore, the pair of linear equations has no solution.

Question 5.
Value(s) of k for which the quadratic equation 2x ² – kx + k = 0 has equal roots is
(a) only 0
(b) 4
(c) only 8
(d) 0, 8
Answer:
(d) 0, 8

Since, the given quadratic equation 2x ² – kx + k = 0 has equal roots.
Discriminant, (-k) ² – 4(2)(k) = 0
⇒ k ² -8k = 0
⇒ k(k – 8) = 0
⇒ k = 0 or k = 8

Question 6.
The distance of the point (3, 5) from the x-axis is k units, then k equals: 1
(a) 3
(b) 4
(c) 5
(d) 8
Answer:
(c) 5
Explanation: The distance of point (3, 5) from the x-axis is equal to the ordinate of the given coordinates. So, the distance from the x-axis is 5 units.

Question 7.
If in ΔABC and ΔPQR, we have \(\frac{A B}{Q R}=\frac{B C}{P R}=\frac{C A}{P Q}\), then
(a) ΔPQR ~ ΔCAB
(b) ΔPQR ~ ΔABC
(c) ΔCBA ~ ΔPQR
(d) ΔBCA ~ ΔPQR
Answer:
(a) ΔPQR ~ ΔCAB

Given, in ΔABC and ΔPQR,
\(\frac{A B}{Q R}=\frac{B C}{P R}=\frac{C A}{P Q}\)
The corresponding sides of ACAB and A PQR are in the same ratio.
∴ Δ PQR ~ Δ CAB

Question 8.
Which of the following is NOT a similarity criterion of triangles? 1
(a) AA
(b) SAS
(c) AAA
(d) RHS
Answer:
(d) RHS
Explanation: RHS is not a similarity criterion, it is a congruence criterion.

Question 9.
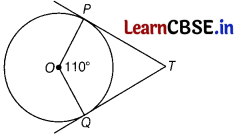
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to

(a) 60°
(b) 70°
(c) 80°
(d) 90°
Answer:
(b) 70°

PT ⊥ OP and QT ⊥ OQ
[∵ tangent to a circle is perpendicular to the radius through the point of contact]
⇒ ∠OPT = 90°
and ∠OQT = 90°
Now, in quadrilateral OQTP,
∠O + ∠Q + ∠T + ∠P = 360°
[angle sum property of quadrilateral]
⇒ 110° + 90°+ ∠T + 90° = 360°
⇒ ∠T = 70°
or ∠PTQ = 70°

Question 10.
If cos A = g , then tan A is: 1
(a) \(\frac{3}{5}\)
(b) \(\frac{3}{4}\)
(c) \(\frac{4}{3}\)
(d) \(\frac{1}{8}\)
Answer:
(b) \(\frac{3}{4}\)
Explanation: Given, cos A = \(\frac{4}{5}\)

Question 11.
If the height of the tower is equal to the length of its shadow, then the angle of elevation of the sun is ……………
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Answer:
(b) 45°

Let AB be the tower and BC be its shadow.

Given, AB = BC
In right angled ∆ABC,
tan C = \(\frac{\text { Perpendicuar }}{\text { Base }}\)
= \(\frac{A B}{B C}\) = 1
⇒ tan C = tan 45° [∵ tan 45° = 1]
⇒ C = 45°

Question 12.
(1 – cos ² A) is equal to: 1
(a) sin ² A
(b) tan ² A
(c) 1 – sin ² A
(d) sec ² A
Answer:
(a) sin ² A
Explanation: We know that,
sin ² A + cos ² A = 1
1 – cos ² A = sin ² A

Question 13.
The radius of a circle is same as the side of a square. Their perimeters are in the ratio
(a) 1 : 1
(b) 2 : π
(c) π : 2
(d) √π : 2
Answer:
(c) π : 2

Let the radius of a circle and side of a square be x unit.
Then, perimeter of circle = 2πx
and perimeter of square = 4x
∴ \(\frac{\text { Perimeter of circle }}{\text { Perimeter of square }}=\frac{2 \pi x}{4 x}\)
= \(\frac{\pi}{2}\)

Question 14.
The area of the circle is 154 cm ² . The radius of the circle is: 1
(a) 7 cm
(b) 14 cm
(c) 3.5 cm
(d) 17.5 cm
Answer:
(a) 7 cm
Explanation: Given, area of circle = 154 cm ²
∵ Area of circle = πr ²
πr ² = 154
r ² = 154 × \(\frac{7}{22}\)
r ² = 7 × 7
r = 7 cm
Hence, the radius of circle is 7 cm.

Question 15.
When a dice is thrown once, the probability of getting an even number less than 4 is
(a) 1/4
(b) 0
(c) 1/2
(d) 1/6
Answer:
(d) 1/6

Let E be the event of getting an even number less than 4.
Outcomes favourable to E : {2}
Possible outcomes: {1, 2, 3, 4, 5, 6}
∵ P(E) = Number of outcomes favourable to E / Total number of possible outcomes
= \(\frac{1}{6}\)

Question 16.
For the following distribution: 1

Class	Frequency
0 – 5	10
5 – 10	15
10 – 15	12
15 – 20	20
20 – 25	9

The Lower limit of modal class is:
(a) 15
(b) 20
(c) 10
(d) 5
Answer:
(a) 15
Explanation:

Class	Frequency	Cumulative Frequency
0 – 5	10	10
5 – 10	15	25
10 – 15	12	37
15 – 20	20	57
20 – 25	9	66

The highest frequency is 20, which lies in the interval 15 – 20.
So, the lower limit of modal class is 15.

Question 17.
A rectangular sheet of paper 40 cm × 22 cm, is rolled to form a hollow cylinder of height 40cm. The radius of the cylinder (in cm) is
(a) 3.5
(b) 7
(c) \(\frac{80}{7}\)
(d) 5
Answer:
(a) 3.5

Let r be the radius of cylinder.

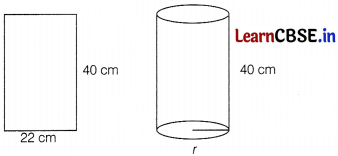
After the sheet is folded, the breadth of the rectangular sheet will become the perimeter of the base of the cylinder.
∴ 22 = 2πr
r = \(\frac{22 \times 7}{22 \times 2}\)
r = \(\frac{7}{2}\) = 3.5 cm

Question 18.
Consider the following frequency distribution: 1

Class	Frequency
0 – 6	12
6 – 12	10
12 – 18	15
18 – 24	8
24 – 30	11

The median class is:
(a) 6 – 12
(b) 12 – 18
(c) 18 – 24
(d) 24 – 30
Answer:
(b) 12 – 18
Explanation:

Class	Frequency	Cumulative Frequency
0 – 6	12	12
6 – 12	10	22
12 – 18	15	37
18 – 24	8	45
24 – 30	11	56

Here, N = 56
∴ \(\frac{N}{2}=\frac{56}{2}\) = 28, which Lies in the interval 12 – 18.

Question 19.
Assertion (A) The point (0, 5) lies on x-axis.
Reason (R) The x-coordinate of the point on x-axis is zero.
(a) Both Assertion and Reason are true and Reason is the correct explanation of Assertion.
(b) Both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
(c) Assertion is true but Reason is false
(d) Assertion is false but Reason is true
Answer:
(a) Both Assertion and Reason are true and Reason is the correct explanation of Assertion.

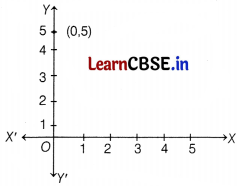
Given point is (0, 5), abscissa (x – coordinate) is 0 and ordinate (y – coordinate) is 5.

Question 20.
Assertion (A): The HCF of two numbers is 5 and their product is 150. Then their LCM is 40.
Reason (R): For any two positive integers a and b, HCF (a, b) × LCM (a, b) = a × b. 1
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Answer:
(d) Assertion (A) is false but reason (R) is true.
Explanation: We know that
HCF (a, b) × LCM (a, b) = a × b
Given that HCF (a, b) = 5
a × b = 150
5 × LCM (a, b) = 150
LCM (a, b) = \(\frac{150}{5}\)
LCM (a, b) = 30

Section – B
Section B consists of 5 Questions of 2 marks each.

Question 21.
Find whether the following pair of linear equations is consistent or inconsistent 3x + 2y = 8, 6x – 4y = 9.
Answer:
Given, pair of linear equation is 3x + 2y = 8
⇒ 3x + 2y – 8 = 0
and 6x – 4y = 9
⇒ 6x – 4y – 9 = 0
Here, \(\frac{a_1}{a_2}=\frac{3}{6}=\frac{1}{2}\)
and \(\frac{b_1}{b_2}=\frac{2}{-4}=\frac{-1}{2}\)
[where a ₁ , a ₂ are coefficients of x and b ₁ , b ₂ are coefficients of y]
∵ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
The pair of linear equations is consistent.

Question 22.
In the given figure, if ABCD is a trapezium in which AB || CD || EF, then prove that \(\frac{A E}{E D}=\frac{B F}{F C}\). 2

OR
In figure, if AD = 6 cm, DB = 9 cm, AE = 8 cm and EC = 12 cm and ∠ADE = 48°. Find ∠ABC.

Answer:
Given:-AB || CD || EF
To prove:- \(\frac{A E}{E D}=\frac{B F}{F C}\)
Construction:- Join BD to intersect EF at G.

OR
Given AD = 6 cm, DB = 9 cm AE = 8 cm, EC = 12 cm, ∠ADE = 48 To find:- ∠ABC=?

Proof:
In ΔABC
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{6}{9}=\frac{2}{3}\) ………. (i)
\(\frac{A E}{E C}=\frac{8}{12}=\frac{2}{3}\) ………. (ii)
From (i) and (ii)
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
DE || BC [Converse of BPT]
∠ADE = ∠ABC [Corresponding angles]
⇒ ∠ABC = 48°

Question 23.
The length of a tangent from a point A at distance 5cm from the centre of the circle is 4cm. Find the radius of the circle.
Answer:
Let O be the center of circle
and let B be the point of contact of tangent and circle

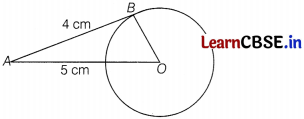
OB ⊥ AB
[∵ tangent to a circle is perpendicular to the radius through the point of contact]
In right angled ∆OBA,
OA ² = OB ² + AB ²
5 ² = OB ² + 4 ²
OB ² = 25 – 16
OB ² = 9
⇒ OB = 3 cm

Question 24.
Evaluate: sin ² 60° + 2tan 45° – cos ² 30°. 2
Answer:
sin ² 60° + 2 tan 45° – cos ² 30°
= (\(\frac{\sqrt{3}}{2}\)) ² + 2(1) – (\(\frac{\sqrt{3}}{2}\)) ²
= \(\frac{3}{4}\) + 2 – \(\frac{3}{4}\)
= 2

Question 25.
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of radius 40 cm and 9 cm?
Answer:
Let radius of two circles be r ₁ and r ₂
and let r be the radius of big circle.
Given, r ₁ = 40 cm
r ₂ = 9 cm
According to the question,
πr² = πr ₁ ² + πr ₂ ²
r ² = r ₁ ² + r ₂ ²
= 40 ² + 9 ²
= 1600 + 81 = 1681
r = \(\sqrt{1681}\) = 41 cm
:. Diameter of the required circle = 2r
= 2 × 41 = 82 cm

Or

A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of minor segment (use π = 3.14)
Answer:
Given, radius of a circle is 10 cm.

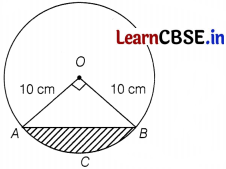
∴ Area of minor segment ACB = Area of sector OACB – Area of tOAB
Area of sector OACB = \(\frac{90}{360}\) π × (radius) ²
= \(\frac{1}{4}\) × 314 × (10) ²
= 78.5 cm ²
∴ Area of ∆OAB, = \(\frac{1}{2}\) × Base × Height
= \(\frac{1}{2}\) × QA × QB
= \(\frac{10 \times 10}{2}\) = 50 cm
∴ Required area = 78.5 – 50 = 28.5 cm ²

Section – C
Section C consists of 6 Questions of 3 marks each

Question 26.
Prove that \(\sqrt{3}\) is an irrational number. 3
Answer:
Let us assume that \(\sqrt{3}\) be a rational number \(\sqrt{3}=\frac{a}{b}\) where a and b are co-prime, squaring both the sides
(\(\sqrt{3}\)) ² =(\(\frac{a}{b}\)) ²
3 = \(\frac{a^2}{b^2}\)
⇒ a ² = 3b ²
a ² is divisible by 3, so a is also divisible by 3 …(i)
Let, a = 3c for any integer c.
(3c) ² = 3b ²
9c ² =3b ²
b ² = 3c ²
Since b ² is divisible by 3 so, b is also divisible by 3 …(ii)
From (i) & (ii) we can say that 3 is a factor of a and b which contradicts the fact that a and b are co-prime.
Thus, our assumption that \(\sqrt{3}\) is a rational number is wrong.
Hence, \(\sqrt{3}\) is an irrational number.

Question 27.
Find the zeroes of the quadratic polynomial 4s ² – 4s + 1 and verify the relationship between the zeroes and the coefficients.
Answer:
Let f(s) = 4s ² – 4s + 1
= 4s ² – 2s – 2s + 1
= 2s (2s – 1) – 1 (2s – 1)
For zeroes of f(s), put f(s) = 0
⇒ (2s – 1) (2s – 1) = 0
⇒ s = \(\frac{1}{2}\), \(\frac{1}{2}\)
Now, sum of zeroes = \(\frac{1}{2}+\frac{1}{2}\) = 1
and product of zeroes = \(\frac{1}{2} \times \frac{1}{2}=\frac{1}{4}\)
We know,
sum of zeroes = \(\frac{- \text { Coefficient of } s}{\text { Coefficient of } s^2}\)
= – \(\frac{(-4)}{4}\) = 1
and product of zeroes = \(\frac{\text { Constant term }}{\text { Coefficient of } s^2}\)
= \(\frac{1}{4}\)

Question 28.
The coach of a cricket team buys 4 bats and 1 ball for ₹ 2050. Later, she buys 3 bats and 2 balls for 1600. Find the cost of each bat and each ball.
OR
A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid ₹27 for a book kept for seven days, while Susy paid ₹21 for the book she kept for five days. Find the fixed charge and the charge for each extra day. 3
Answer:
Let the cost of one bat be ₹ x
Let the cost of one ball be ₹ y
ATQ
4x + 1y = 2050 …….. (i)
3x + 2y = 1600 …….. (ii)
from (i) 4x + 1y = 2050
y = 2050 – 4x
Substitute value of y in (ii)
3x+ 2(2050 – 4x) = 1600
3x + 4100 – 8x =1600
-5x= -2500
x= 500
Substitute value of x in (i)
4x + 1y = 2050
4(500) + y = 2050
2000 + y = 2050
y = 50
Hence
Cost of one bat = ₹ 500
Cost of one ball = ₹ 50
OR
Let the fixed charge for first 3 days = ₹ x
And additional charge after 3 days = ₹ y
ATQ
x + 4y = 27 ……… (i)
x + 2y = 21 …….. (ii)
Subtract eqn (ii) from (i)
2y = 6
y = 3
Substitute value of y in (ii)
x + 2(3) = 21
x= 21 – 6
x = 15
Fixed charge = ₹ 15
Additional charge per day = ₹ 3

Question 29.
A circle touches all four sides of quadrilateral ABCD. Prove that AB + CD = AD + BC.
Answer:
Let the circle intersects AB, BC, CD and DA at point L,M, N, and O respectively.

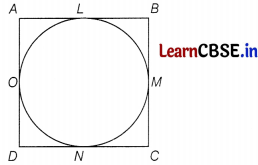
Now, AL = LO …………(i)
[∵ tangents from an external point to circle are equal in Length]
Similarly, DN = DO ………….(ii)
CN = CM ………..(iii)
BL = BM …………(iv)
On adding Eqs. (i), (ii), (iii) and (iv), we get
AL + DN + CN + BL = AO + DO + CM + BM
⇒ (AL + BL) + (DN + CN) = (AO + DO) + (CM + BM)
⇒ AB + CD = AD + BC
[∵ AL + BL = AB,
DN + CN = CD,
AO + DO = AD
CM + BM = BC]

Question 30.
Prove that: (cosec θ – cot θ) ² = \(\frac{1-\cos \theta}{1+\cos \theta}\)
OR
Prove that sec A (1 – sin A) (sec A + tan A) = 1. 3
Answer:

LHS = RHS,
Hence Proved.
OR
sec A (1 – sin A) (sec A + tan A) = 1

= 1 = R.H.S
L.H.S = R.H.S
Hence Proved.

Question 31.
A bag contains 6 red, 4 black, and some white balls.

(i) Find the number of white balls in the bag, if the probability of drawing a white ball is 1/3.
Answer:
Let the number of white balls be n.
Total number of balls = 6 + 4+ n = 10 + n
Let E be the event of drawing a white ball.
Given, P(E) = \(\frac{1}{3}\)
⇒ \(\frac{\text { Number of outcomes favourable to } E}{\text { Total number of outcomes }}=\frac{1}{3}\)
⇒ \(\frac{n}{10+n}=\frac{1}{3}\)
⇒ 3n = 10 + n
⇒ 2n = 10
⇒ n = 5

(ii) How many red balls should be removed from the bag for the probability of drawing a white ball to be \(\frac{1}{2}\)?
Answer:
Now, total number of balls = 10 + n
= 10 + 5 = 15
Let x red balls are removed from the bag.
∴ Total number of balls in the the bag = 15 – x
Now, P(E) = \(\frac{1}{2}\)
⇒ \(\frac{5}{15-x}=\frac{1}{2}\)
⇒ 10 = 15 – x
⇒ x = 5

Section – D
Section D consists of 4 Questions of 5 marks each

Question 32.
A train travels 360 km at a uniform speed. If the speed had been 5 km/hr more, it would have taken 1 hour less for the same journey. Find the speed of the train.
OR
A motor boat whose speed is 18 km/h in still water takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream. 5
Answer:
Let the speed of train be × km/hr
distance = 360 km
Speed = \(\frac{\text { distance }}{\text { time }}\)
Time = \(\frac{360}{x}\)
New speed = (x + 5) km/hr
Time = \(\frac{D}{5}\)
x + 5 = \(\frac{360}{\left(\frac{360}{x}-1\right)}\)
(x + 5)(\(\frac{360}{x}\) – 1) = 360
(x + 5)(360 – x) = 360x
-x ² – 5x + 1800 = 0
x ² + 5x – 1800 = 0
x ² + 45x – 40x – 1800 = 0
x(x + 45) – 40(x + 45) = 0
(x + 45)(x – 40) = 0
x + 45 = 0, x – 40 = 0
x = -45, x = 40
Speed cannot be negative
Speed of train = 40km/hr
OR
Let the speed of the stream = xkm/hr
Speed of boat = 18 km/hr
Upstream speed = (18 – x)km/hr
Downstream speed =(18 + x) km/hr
Time taken (upstream) = \(\frac{24}{(18+x)}\)
Time taken (downstream) = \(\frac{24}{(18-x)}\)
ATQ
\(\frac{24}{(18-x)}=\frac{24}{(18+x)}\) + 1
\(\frac{24}{(18-x)}-\frac{24}{(18+x)}\) = 1
24(18 + x) – 24(18 – x)= (18 – x)(18 + x)
24(18 + x – 18 + x) = (18) ² – x ²
24(2x) = 324 – x ²
48x – 324 + x ² = 0
x ² + 48x – 324 = 0
x ² – 6x + 54x – 324 = 0
x(x – 6) + 54(x – 6) = 0
(x – 6) (x + 54) = 0
x – 6 = 0, x + 54 = 0
x = 6 , x = -54
Speed cannot be negative
Speed of stream=6 km/hr

Question 33.
(i) Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Answer:
Let ABC be a triangle in which a line parallel to side BC intersects the other two skies AB and AC at D and E, respectively

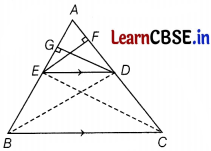
Join BD, CE and draw EF ⊥ AC and DG ⊥ AB
Area of ∆AED = \(\frac{1}{2}\) × Base × Height
= \(\frac{1}{2}\) × AE × GD
ar (∆ AED) = \(\frac{1}{2}\) × AE × GD
Area of ∆BED = ar (∆ BED)
= \(\frac{1}{2}\) × BE × DG
Also, ar (∆ AED) = \(\frac{1}{2}\) × AD × EF
ar (∆ CED) = \(\frac{1}{2}\) × CD × EF
∵ \(\frac{\ {ar}(\triangle A E D)}{\ {ar}(\triangle B E D)}=\frac{\frac{1}{2} \times A E \times G D}{\frac{1}{2} \times B E \times G D}=\frac{A E}{B E}\) ………..(i)
and \(\frac{\ {ar}(\triangle A E D)}{\ {ar}(\triangle C E D)}=\frac{\frac{1}{2} \times A D \times E F}{\frac{1}{2} \times C D \times E F}=\frac{A D}{C D}\) ………….(ii)
since, ∆ BED and ∆ CED are on the same base and between the same parallels.
∴ ar (∆ BED) = ar (∆ CED) ………………(iii)
From Eqs. (i), (ii) and (iii), we have
\(\frac{A E}{E B}=\frac{A D}{D C}\)
Hence proved.

(ii) In ∆ PQR, S and T are points on PQ and PR, respectively. If \(\frac{P S}{S Q}=\frac{P T}{T R}\) and ∠PST = ∠PRQ, then prove that PQR is an isosceles triangle.
Answer:
Given, \(\frac{P S}{S Q}=\frac{P T}{T R}\)

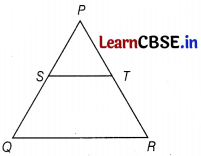
By converse of BPT,
ST || QR
⇒ PO is the transversal.
∴ ∠PST = ∠POR [corresponding angles]
Given, ∠PST = ∠PRQ
∠PQR = ∠PRQ
⇒ PQ = PR
[sides opposite to equal angles are equal]
∴ ∆ PQR is an isosceles triangle.

Question 34.
A medicine capsule is in the shape of a cylinder with two hemispheres stuck at each of its ends. The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.

OR
A gulab jamun, contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like cylinder with two hemisphericaL ends with Length 5 cm and diameter 2.8 cm.

Answer:
Diameter of cylinder and hemisphere = 5 mm
Radius, (r) = \(\frac{5}{2}\)
Total length = 14 mm
Height of cylinder = 14 – 5 = 9 mm
CSA of cylinder = 2πrh
= 2 × \(\frac{22}{7}\) × \(\frac{5}{2}\) × 9
= \(\frac{990}{7}\)mm ²
CSA of hemispheres = 2πr ²
= 2 × \(\frac{22}{7}\) × (\(\frac{5}{2}\)) ²
= \(\frac{275}{7}\) mm ²
CSA of 2 hemispheres = 2 × \(\frac{275}{7}\)
= \(\frac{550}{7}\) mm ²
Total area of capsule = \(\frac{990}{7}+\frac{550}{7}\)
= \(\frac{1540}{7}\)
= 220 mm ²
OR
Diameter of cylinder = 2.8 cm
radius of cylinder = \(\frac{2.8}{2}\) = 1.4 cm
Radius of cylinder = Radius of hemisphere
= 1.4 cm
Height of cylinder = 5 – 2.8
= 2.2 cm
Volume of 1 Gulab jamun
= vol. of cylinder + 2 × vol. of hemisphere
= πr ² h + 2 × \(\frac{2}{3}\)πr ³
= \(\frac{22}{7}\) (1.4) ² × 2.2 + 2 × \(\frac{2}{3}\) × \(\frac{22}{7}\) × (1.4) ³
= 13.55 + 11.50
= 25.05 cm ³
Volume of 45 Gulabjamun = 45 × 25.05
Syrup in 45 Gulabjamun = 30% × 45 × 25.05
= \(\frac{30}{100}\) × 45 × 25.05 1
= 338.175 cm ³
≈ 338 cm ³

Question 35.
The following table gives the distribution of the lifetime of 400 neon lamps

Lifetime (in hours)	Number of lamps
1500 – 2000	14
2000 – 2500	56
2500 – 3000	60
3000 – 3500	86
3500 – 4000	74
4000 – 4500	62
4500 – 5000	48

Find the average life time of a lamp.
Answer:

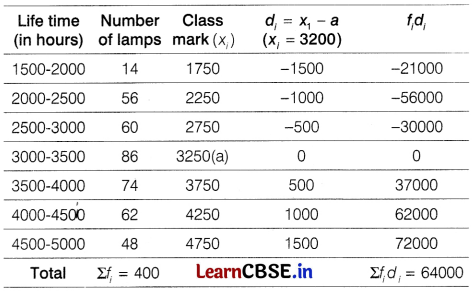
Assumed mean, a = 3250
∴ \(\bar{x}=a+\frac{\Sigma f_i d_i}{\Sigma f_i}\)
= 3250 + \(\frac{64000}{400}\)
= 3250 + 160 = 3410

Section – E
Section E consists of 3 Questions of 2 marks each

Question 36.

Case Study 1

India is competitive manufacturing location due to the low cost of manpower and strong technical and engineering capabilities contributing to higher quality production runs. The production of TV sets in a factory increases uniformly by a fixed number every year. It produced 16000 sets in 6 ^th year and 22600 in 9 ^th year.

Based on the above information, answer the following questions:
(A) In which year, the production is 29,200 sets? 1
(B) Find the production in the 8 ^th year.
OR
Find the production in first 3 years. 2
(C) Find the difference of the production in 7 ^th year and 4 ^th year. 1
Answer:
a ₆ = 16000, a ₉ = 22600
a + 5d = 16000 ………… (i)
a + 8d = 22600 ………….. (ii)
Substitute a = 1600 – 5d from (i)
16000 – 5d + 8d= 22600
3d = 22600 – 16000
3d = 6600
d = \(\frac{6600}{3}\) = 2200
a = 16000 – 5(2200)
a = 16000 – 11000
a = 5000

(A) a _n = 29200, a = 5000, d = 2200
= a _n + (n – 1)d
29200 = S000+(n – 1) 2200
29200 – 5000 = 2200n – 2200
24200 + 2200 = 2200n
26400 = 2200n
n = \(\frac{264}{22}\)
n = 12
In 12 ^th year the production was ₹ 29200

(B) n = 8, a = 5000, d = 2200
a _n = a + (n – 1 )d
= 5000 + (8 – 1) 2200
= 5000 + 7 × 2200
= 5000 + 15400
= 20400

The production during 8 ^th year is 20400
OR
n = 3, a = 5000,d = 2200
S _n = \(\frac{n}{2}\)[2a + (n – 1)d]
= \(\frac{3}{2}\)[2(5000) + (3 – 1)2200]
S ₃ = \(\frac{3}{2}\)(10000 + 2 × 2200)
= 3 × 7200
= 21600

(C) a ₄ = a + 3d
= 5000 + 3 (2200)
= 5000 + 6600
= 11600
a ₇ = a + 6d
= 5000 + 6 × 2200
= 5000 + 13200
= 18200
a ₇ – a ₄ = 18200 – 11600 = 6600

Question 37.

Case Study 2

Alia and Shagun are friends living on the same street in Patel Nagar. Shagun’s house is at the intersection of one street with another street on which there is a library. They both study in the same school and that is not far from Shagun’s house. Suppose the school is situated at the point O i.e. the origin. Alia’s house is at A,. Shagun’s house is at B and library is at C.

Based on the above information, answer the following questions.

(i) How far is Alia’s house from Shagun’s house?
Answer:

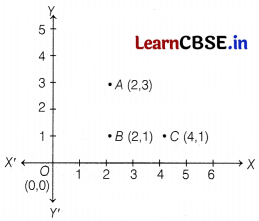
Distance between Alias house and Shaguns house
AB = \(\sqrt{(2-2)^2+(1-3)^2}\)
= \(\sqrt{(-2)^2}\) = 2 units
[∵ distance between two points P(x ₁ , y ₁ ) and Q (x ₂ , y ₂ )
PQ = \(\left.\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\right]\)

(ii) How far is the library from Shagun’s house?
Answer:
Distance between library and shagun’s house
BC = \(\sqrt{(2-4)^2+(1-1)^2}\)
= \(\sqrt{(-2)^2+0}\)
= √4
= 2 units

(iii) Show that for Shagun’s house, school is farther as compared to Alia’s house and library.
Answer:
Distance between Alia’s house and library,
AC = \(\sqrt{(4-2)^2+(1-3)^2}=\sqrt{2^2+(-2)^2}\)
= 2√2 units
Distance between Shagun’s school and Shaguns house = OB
= \(\sqrt{(2-0)^2+(1-0)^2}\)
= \(\sqrt{4+1}=\sqrt{5}\) units
∵ OB > AC
For Shaguns house, school is farther compared to Alia’s house and library.

Or

Show that Alia’s house, Shagun’s house and library form an isosceles right triangle.
Answer:
Distance between Shaguns house and library = \(\sqrt{(4-2)^2+(1-1)^2}\)
= 2 units
Now, AC ² = 8 units
and AB ² + BC ² = 2 ² + 2 ² = 8 units
∴ AC ² = AB ² + BC ²
⇒ ABC is a right angled triangle, right angled at B.
Also, AB = BC = 2 units
∴ ABC is an isosceles right angled triangle.

Question 38.

Case Study 3

A boy is standing on the top of Light house. He observed that boat P and boat Q are approaching the Light house from opposite directions. He finds that angLe of depression of boat P is 45° and angLe of depression of boat Q is 30°. He aLso knows that height of the Light house is 100 m.

Based on the above information, answer the following questions:
(A) What is the measure of ∠APD?. 1
(B) If ∠YAQ = 30°, then ∠AQD is also 30°, Why? 1
(C) Find length of PD.
OR
Find length of DQ. 2
Answer:
(A) XY || PQ and AP is transversal.
∠APD = ∠PAX [Alternative interior angles]
∠APD = 45°

(B) Since, XY || PQ and AQ is a transversal So, alternate interior angles are equal Hence, ∠YAQ = ∠AQD = 30°

(C) In ΔADP, θ = 45°
tan θ = \(\frac{P}{B}\)
tan 45° = \(\frac{100}{P D}\)
PD = 100 m
Boat P is 100 m from the light house
OR
In ΔADQ, Φ = 30°
tan Φ = \(\frac{P}{B}\)
tan 30° = \(\frac{100}{\mathrm{DQ}}\)
\(\frac{1}{\sqrt{3}}=\frac{100}{\mathrm{DQ}}\)
DQ = 100√3 m