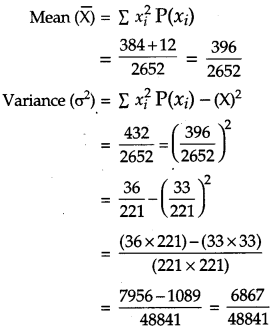CBSE Previous Year Question Papers Class 12 Maths 2019 Delhi
Time allowed: 3 hours
Maximum marks : 100
General Instructions:
- All questions are compulsory.
- The question paper consists of 29 questions divided into four sections A, B, C and D. Section A comprises of 4 questions of one mark each, Section B comprises of 8 questions of two marks each, Section C comprises of 11 questions of four marks each and Section D comprises of 6 questions of six marks each.
- All questions in Section A are to be answered in one word, one sentence or as per the exact requirement of the question.
- There is no overall choice. However, internal choice has been provided in 1 question of Section A, 3 questions of Section B, 3 questions of Section C and 3 questions of Section D. You have to attempt only one of the alternatives in all such questions.
- Use of calculators is not permitted. You may ask for logarithmic tables, if required.
**Answer is not given due to the change in present syllabus
CBSE Previous Year Question Papers Class 12 Maths 2019 Delhi Set I
Section – A
Question 1.
If A and B are square matrices of the same order 3, such that | A | = 2 and AB = 2I, write the value of |B|. [1]
Solution:
Given, | A | = 2 and AB = 2I
∴ | A | =21
⇒ | A | | B | = 2I
⇒ 2|B | = 2I
⇒ | B | = I
Question 2.
If f(x) = x + 1, find \(\frac{d}{d x}(f o f)(x)\). [1]
Solution:
Given, f(x) = x + 1
Now, f
0
f(x) = f(f(x)
= f(x + 1)
= x + 1 + 1
= x + 2
∴ \(\frac{d}{d x}(f o f)(x)\) = 1
Question 3.
Find the order and the degree of the differential equation \(x^{2} \frac{d^{2} y}{d x^{2}}=\left\{1+\left(\frac{d y}{d x}\right)^{2}\right\}^{4}\). [1]
Solution:
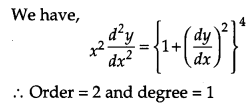
Question 4.
If a line makes angles 90°, 135°, 45° with x, y and z axes respectively, find its direction cosines. [1]
Solution:
Given, α = 90°, β = 135°, γ = 45°
So, l = cos 90° = 0
m = cos135° – cos(180° – 45°)
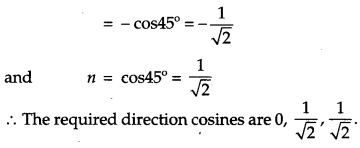
OR
Find the vector equation of the line which passes through the point (3, 4, 5) and is parallel to the vector \(2 \hat{i}+2 \hat{j}-3 \hat{k}\). [1]
Solution:
Given, the line passes through the point (3, 4, 5).
and parallel to the vector \(2 \hat{i}+2 \hat{j}-3 \hat{k}\).
D. R. s of the given vector are < 2, 2, – 3 >.
∴ Vector equation of line,
\(\vec{r}=(3 \hat{i}+4 \hat{j}+5 \hat{k})+\lambda(2 \hat{i}+2 \hat{j}-3 \hat{k})\)
Section – B
Question 5.
Examine whether the operation * defined on R by a * b = ab + 1 is (i) a binary or not. (ii) if a binary operation, is it associative or not?** [2]
Question 6.
Find a matrix A such that 2A – 3B + 5C = 0, where B = \(\left[\begin{array}{rrr}{-2} & {2} & {0} \\ {3} & {1} & {4}\end{array}\right]\) and C = \(\left[\begin{array}{rrr}{2} & {0} & {-2} \\ {7} & {1} & {6}\end{array}\right]\). [2]
Solution:
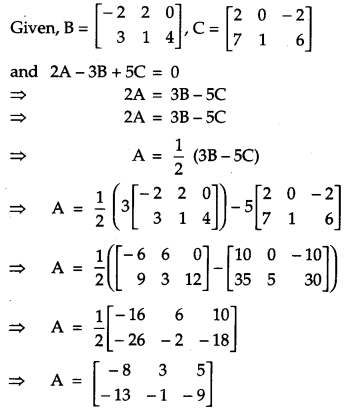
Question 7.
Find: \(\int \frac{\sec ^{2} x}{\sqrt{\tan ^{2} x+4}} d x\). [2]
Solution:
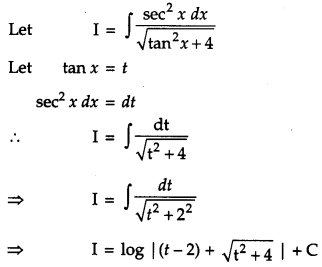
![]()
Question 8.
Find: [2]
![]()
Solution:
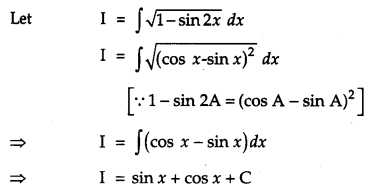
OR
Find: \(\int \sin ^{-1}(2 x) d x\). [2]
Solution:
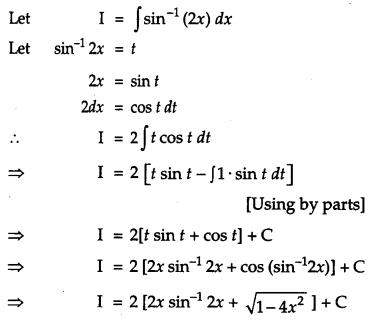
Question 9.
Form the differential equation representing the family of cures y = e
2x
(a + bx), where ‘a’ and ‘b’ are arbitrary constants. [2]
Solution:
Given, y = e
2x
(a +bx) …(i)
Differentiating w.r.t. x, we get
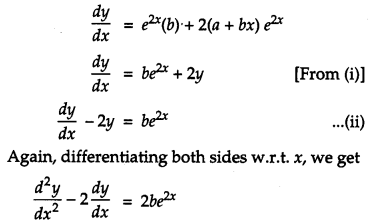
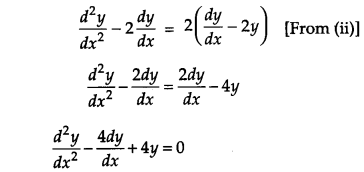
This is the required differential equation.
Question 10.
If the sum of two unit vectors is a unit vector, prove that the magnitude of their difference is \( \sqrt{{3}} \). [2]
Solution:
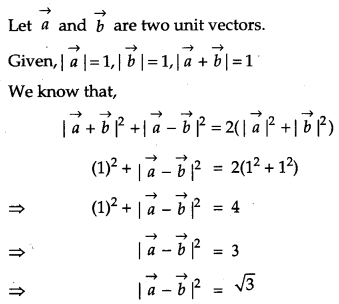
OR
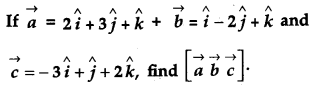 [2]
[2]
Solution:
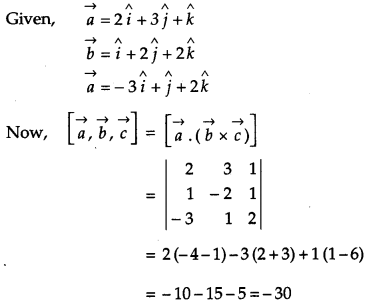
Question 11.
A die marked 1,2,3 in red and 4,5,6 in green is tossed. Let A be the event “number is even”and B be the event “number is marked red”. Find whether the events A and B are independent or not. [2]
Solution:
Given, S = {1, 2, 3, 4, 5, 6 }
Let the two events be
A : The number is even
B : The number is red
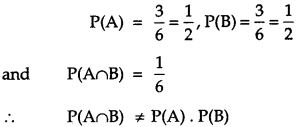
Hence, A and B are ot independent
Question 12.
A die is thrown 6 times. If “getting an odd number” is a “success”, what is the probability of
(i) 5 successes?
(ii) atmost 5 success? [2]
OR
The random variable X has a probability distribution P(X) of the following form, where ‘k’ is some number
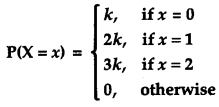
Determine the value of ‘k’. [2]
Solution:
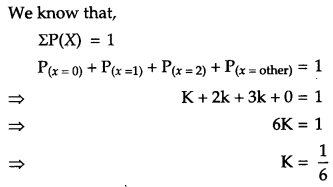
Section – C
Question 13.
Show that the relation R on R defined as R = [(a, b) : a ≤ b], is reflexive, and transitive but not symmetric. [2]
Solution:
Reflexive:
Let a ϵ R
∴ a ≤ a
So, (a, a) ϵ R
Hence, R is reflexive.
Symmetric:
Let (a, b) ϵ R
Then (b, a) ϵ R
Then, a ≤ b
⇒ b ≤ a
∴ (b, a) ∉ R
Hence, R is not symmetric.
Transitive:
Let, a, b, c ϵ R, such that (a, b) ϵ R and (b, c) ϵ R
Then, a ≤ b
and b ≤ c
⇒ a ≤ c
⇒ (a, c) ϵ R
Hence, R is transitive.
Hence, R is reflexive and transitive but not Symmetric. Hence Proved.
OR
Prove that the function f : N → N, defined by f(x) = x
2
+ x + 1 is one-one but not onto.
Find inverse of f : N → S, where S is range of f.
Solution:
Given, f : N → N, f(x) = x
2
+ x +1
Let A be the set of natural number (domain),
and B be the set of natural number (co-domain).
For One-One:
Let x
1
, x
2
ϵ A such that f(x
1
) = f(x
2
)

Not possible since domain = N
So, f is not onto.
Hence, f is one-one but not onto. Hence Proved
Now, f : N → S : f(x) = x
2
+ x + 1
where S = range (Given)
f : N → S is onto as co-domain = range.
Hence, f is invertible.
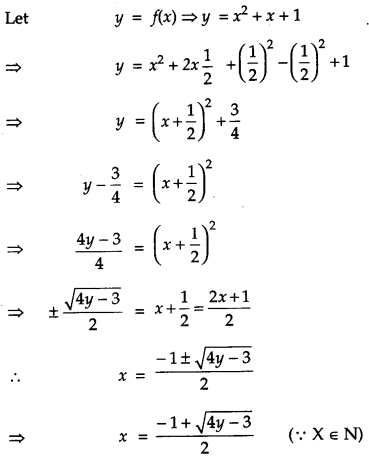
Question 14.
Solve : tan
-1
4x + tan
-1
6x = \(\frac{\pi}{4}\) [2]
Solution:
We have
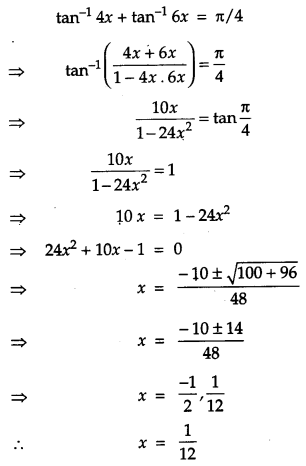
Question 15.
Using properties of determinants, prove that [2]
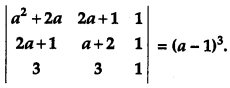
Solution:
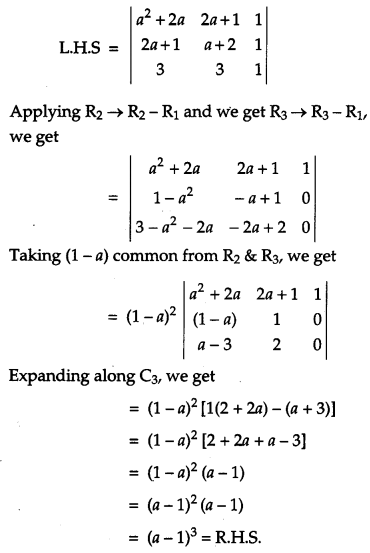
Question 16.
If log(x
2
+ y
2
) = 2 tan
-2
\(\left(\frac{y}{x}\right)\), show that [2]
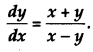
Solution:
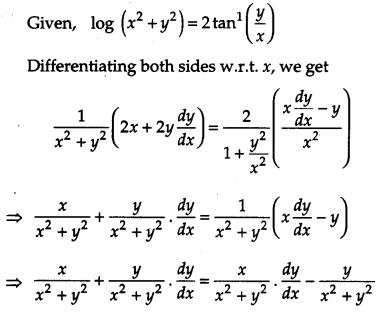
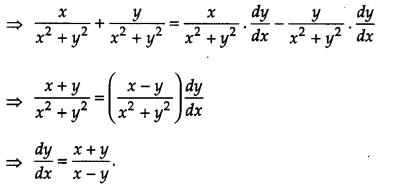
OR
If x
y
– y
x
= a
b
, find \(\frac{d y}{d x}\)
Solution:
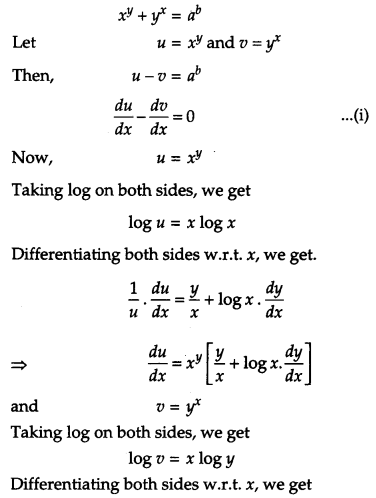
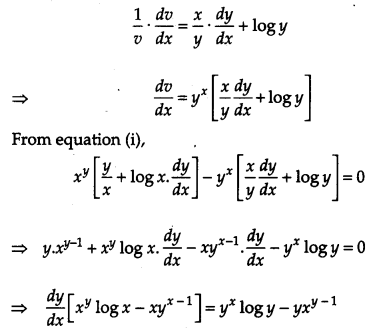
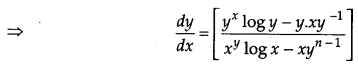
Question 17.
If y = (sin
-1
x)
2
, prove that [2]
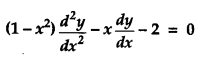
Solution:

Question 18.
Find the equation of tangent to the curve y = \(\sqrt{3 x-2}\) which is parallel to the line 4x – 2y + 5 = 0. Also, write the equation of normal to the curve at the point of contact. [2]
Solution:

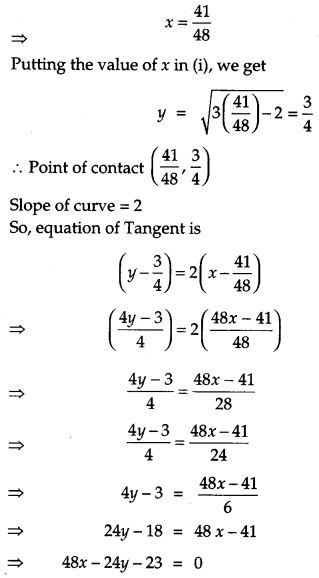
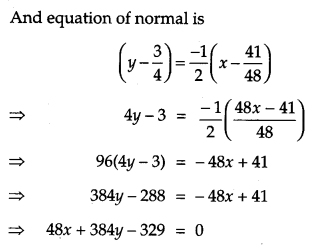
Question 19.
Find: \(\int \frac{3 x+5}{x^{2}+3 x-18} d x\). [2]
Solution:

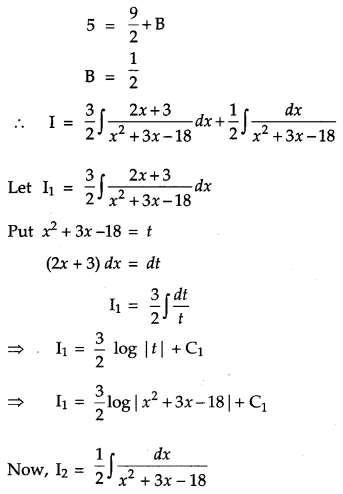
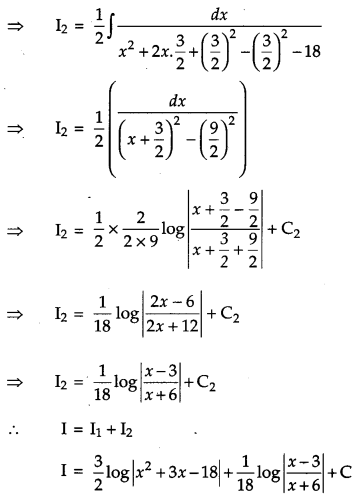
Question 20.
Prove that \(\int_{0}^{a} f(x) d x=\int_{0}^{a} f(a-x) d x\), hence evaluate [2]
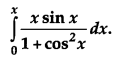
Solution:
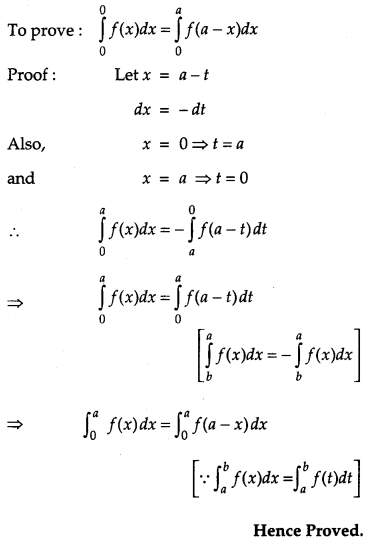

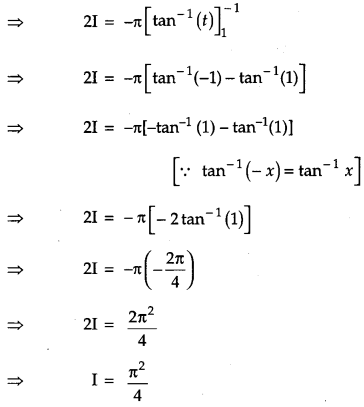
Question 21.
Solve the differential equation xdy – ydx = \(\sqrt{x^{2}+y^{2}} d x\), given that y = 0 when x = 1. [2]
Solution:
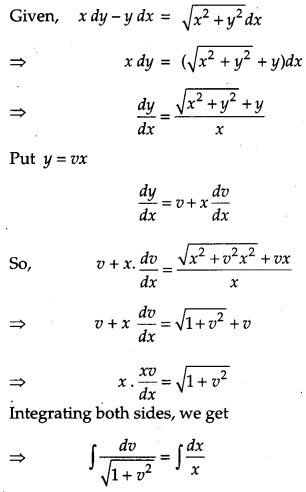
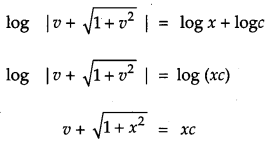
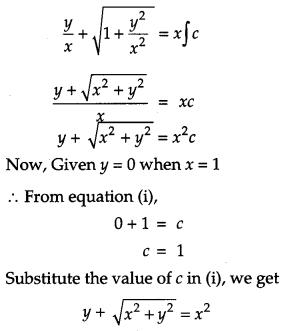
OR
Solve the differential equation (1 + x
2
)\(\frac{d y}{d x}\) + 2xy – 4x
2
= 0, subject to the initial condition y(0) = 0. [2]
Solution:
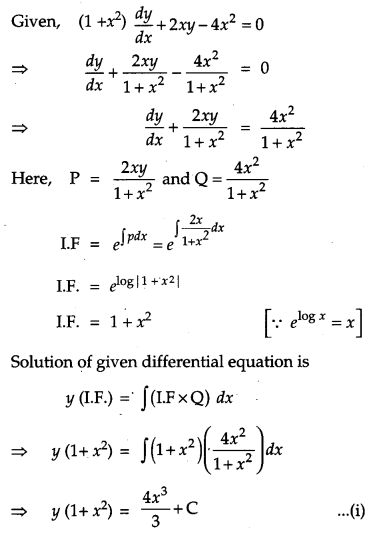
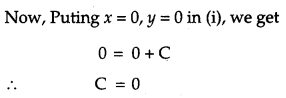
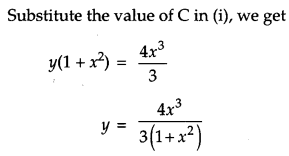
Question 22.
If \(\hat{i}+\hat{j}+\hat{k}, \quad 2 \hat{i}+5 \hat{j}, \quad 3 \hat{i}+2 \hat{j}-3 \hat{k}\) and \(\hat{i}-6 \hat{j}-\hat{k}\) respectively are the position vectors of points A, B, C and D, then find the angle between the straight lines AB and CD. Find whether \(\overrightarrow{\mathrm{AB}} \text { and } \overrightarrow{\mathrm{CD}}\) are collinear or not. [2]
Solution:
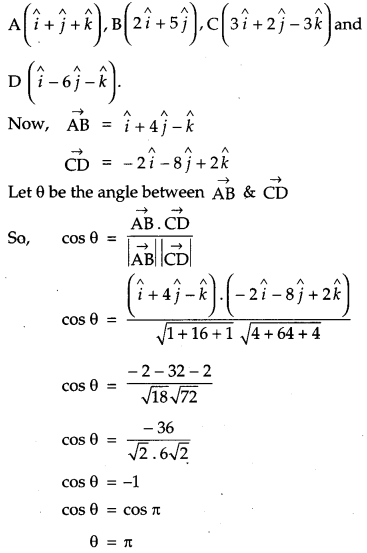
Question 23.
Find the value of λ, so that the line \(\frac{1-x}{3}=\frac{7 y-14}{\lambda}=\frac{z-3}{2} \text { and } \frac{7-7 x}{3 \lambda}=\frac{y-5}{1}=\frac{6-z}{5}\) are at right angles. Also, find whether the lines are intersecting or not. [2]
Solution:
Equation of 1st line,
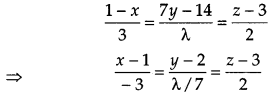
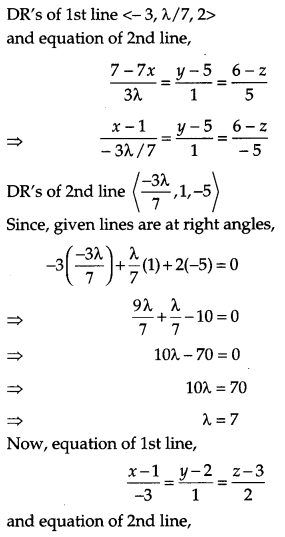
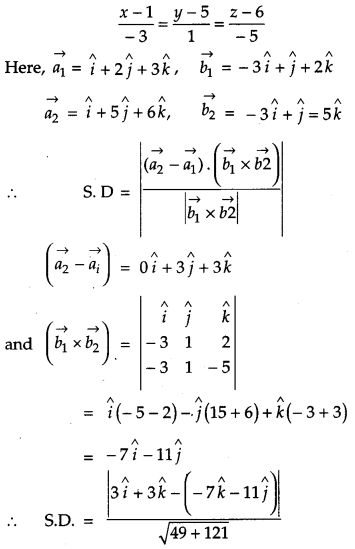
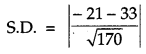
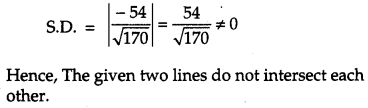
Section – D
Question 24.
If A = \(\left[\begin{array}{lll}{1} & {1} & {1} \\ {1} & {0} & {2} \\ {3} & {1} & {1}\end{array}\right]\), find A
-1
. Hence, solve the system of equations x + y + z = 6, x + 2z = 7, 3x + y + z = 12 [6
Solution:
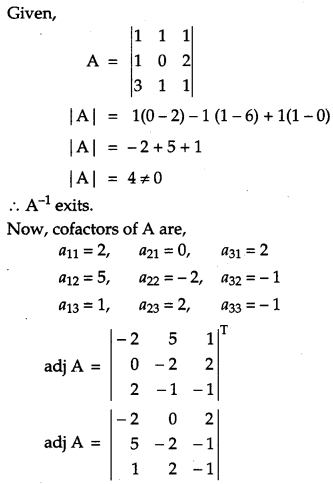
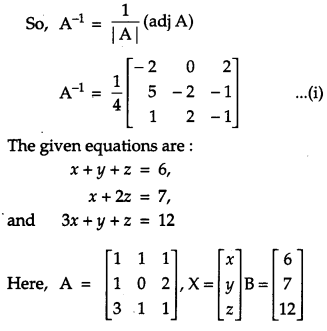
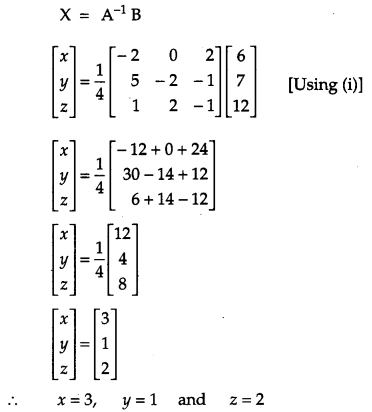
OR
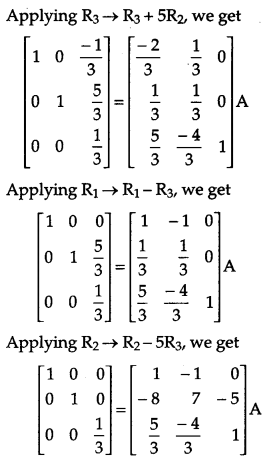
Find the inverse of the following matrix using elementary operations.
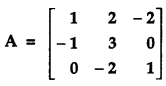
Solution:
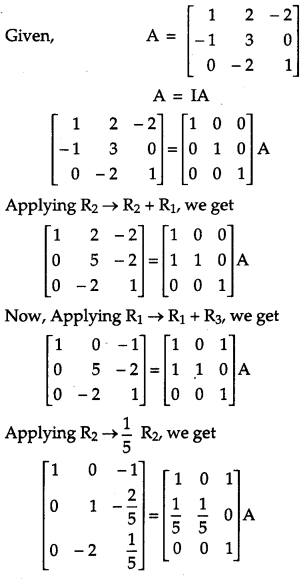
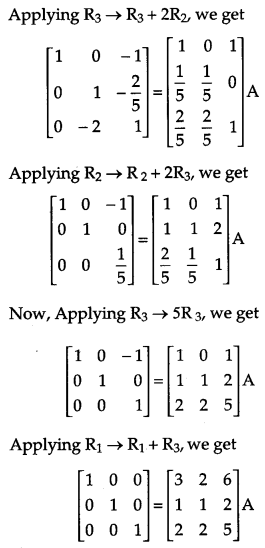
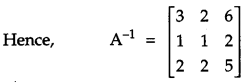
Question 25.
A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m
3
. If building of tank costs ₹ 70 per square metre for the base and ₹ 45 per square metre for the sides, what is the cost of least expresive tank? [6]
Solution:
Let the length and breadth of the tank be x and y metres, respectively.
Given, Volume = 8 m
3
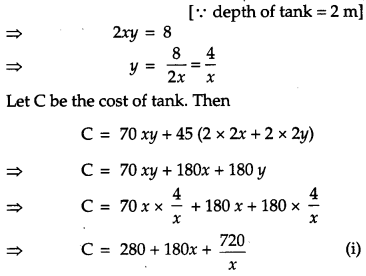

Hence, the cost of least expensive tank is ₹ 1000.
Question 26.
Using integration, find the area of a triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2). [6]
Solution:
Given, A (2, 5), B (4, 7) and C (6, 2) be the vertices of a triangle.
The equation of side AB.
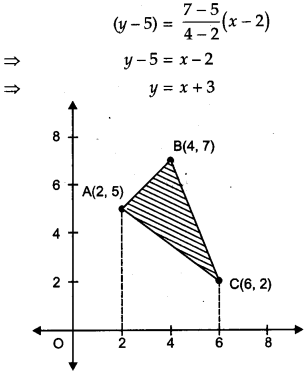
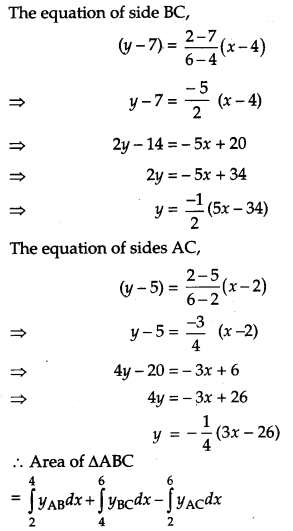
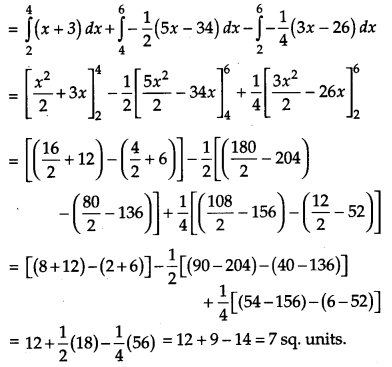
OR
Find the area of a region lying above x-axis and included between the circle x
2
+ y
2
= 8x and inside of the parabola y
2
= 4A:.
Solution:
Given, equation of circle is x
2
+ y
2
= 8x can be expressed as
(x – 4)
2
+ y
2
= 16 …(i)
Centre is (4, 0) and radius is 4 and equation of parabola is y
2
= 4x …(ii)
Let Required Area = I
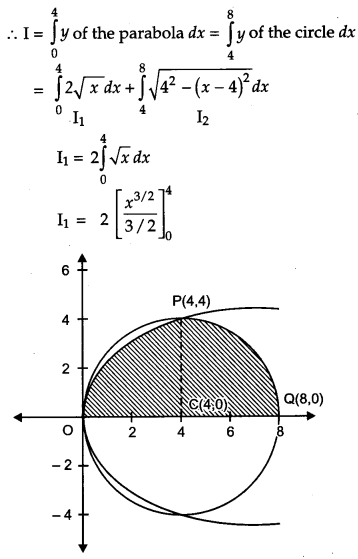
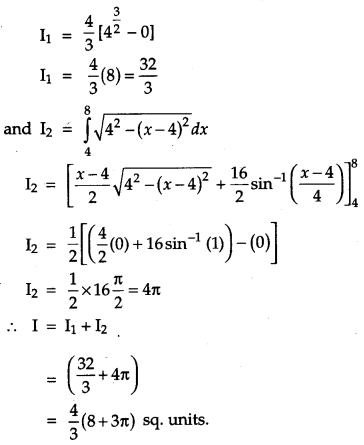
Question 27.
Find the vector and Cartesian equation of the plane passing through the points (2, 2, -1), (3, 4, 2) and (7, 0, 6). Also find the vector equation of a plane passing through (4, 3, 1) and parallel to the plane obtained above. [6]
Solution:
Let A (2, 2, -1), B (3, 4, 2,) and C (7, 0, 6)
The equation of plane passing through A(2, 2, -1),
a(x – 2) + b(y – 2) + c(z + 1) = 0 …(i)
Since (3, 4, 2) and (7, 0, 6) lies on plane
a + 2b + 3c = 0 …(ii)
and 5a – 2b + 7c = 0 …(iii)
Solving equation (ii) and (iii), we get
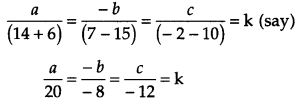
a = 20k, b = 8k and c = -12k
Putting the values of a, b and c in (i), we get
20k(x – 2) + 8k(y – 2) a – 12k (z + 1) = 0
⇒ 4k [5x – 10 + 2y – 4 – 3z – 3] = 0
⇒ 5x + 2y – 3z – 17 = 0
This is the required equation of the plane.
Now, the second plane passes through the points (4, 3, 1).
Since, this plane is parallel to the above plane,
∴ D. R/s of the second plane be < 5, 2, – 3 >
So, equation of second plane,
5(x – 4) + 2(y – 3) – 3(z – 1) = 0
⇒ 5x – 20 + 2y – 6 – 3z + 3 = 0
⇒ 5x + 2y – 3z – 23 = 0
OR
Find the vector equation of the plane that contains the lines \(\vec{r}=(\hat{i}+\hat{j})+\lambda(\hat{i}+2 \hat{j}+\hat{k})\) and the point (-1, 3, – 4). Also, find the length of the perpendicular drawn from the point (2, 1, 4) to the plane, thus obtained.
Solution:
Given, equation of the given line
\(\vec{r}=(\hat{i}+\hat{j})+\lambda(\hat{i}+2 \hat{j}+\hat{k})\)
The plane passes through the point (- 1, 3, -4).
Then the equation of the plane,
a(x + 1) + b (y – 3) + c (z + 4) = 0 …(i)
Since (1, 1) lies on the plane,
∴ 2a – 2b + 4c = 0 …(ii)
Also, (1, 2, -1) lies on the plane
∴ 2a – b + 3c = 0 …(iii)
Solving equations (ii) and (iii), we get

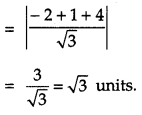
Question 28.
A manufacturer has three machine operators A, B and C. The first operator A produces 1% of defective items, whereas the other two operators B and C produces 5% and 7% defective items respectively. A is on the job for 50% of the time, B on the job 30% of the time and C on the job for 20% of the time. All the items are put into one stockpile and then one item is chosen at random .from his and is found to be defective. What is the probability that it was produces by A? [6]
Solution: .
Let Hi be the event items produced by A
H
2
be the event items produced by B
H
3
be the event items produced by C

Question 29.
A manufacturer has employed 5 skilled men and 10 semi-skilled men and makes two models A and B of an article. The making two one item of model A requires 2 hours work by a skilled man and 2 hours work by a semi-skilled man. One item of model B requires 1 hour by a skilled man and 3 hours by a semi-skilled man. No man is expected to work more than 8 hours per day. The manufacturer’s profit on an item of model A is ₹15 and on an item of model B is ₹ 10. How many of items of each model should be made per day in order to maximize daily profit? Formulate the above LPP and solve it graphically and find the maximum profit. [6]
Solution:
Let, x be the number of items of model A and y be the number of items of model B
Let Z be the required profit.
Subject to constraints:
2x + y ≤ 8 × 5
⇒ 2x + y ≤ 40
2x + 3y ≤ 8 × 10
⇒ 2x + 3y ≤ 80
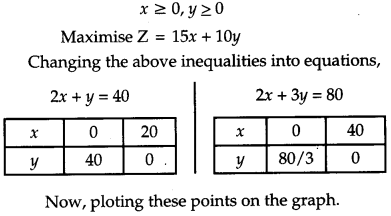
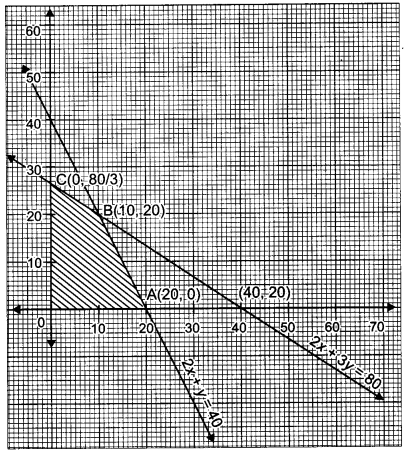

Thus, the maximum profit is obtained when the manufacture produces 10 items of model A and 20 items of model B and the maximum profit ₹ 250.
CBSE Previous Year Question Papers Class 12 Maths 2019 Delhi Set II
Note: Except for the following questions, all the remaining questions have been asked in previous sets.
Section – A
Question 2.
If f(x) = x + 7 and gix) = x – 7, x ϵ R, then find \(\frac{d}{d x}(f \circ g)(x)\)/ [1]
Solution:
Given, f(x) = x + 7
and y(x) = x – 7
Given, (fog) (x) = f(g (x)
= f(x – 7)
= f(x – 7) + 7
= x
Now, Differentiating w.r.t, x, we get
\(\frac{d(f o g)}{d x}(x)=1\)
Question 3.
Find the value of x – y, if
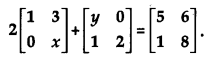
Solution:
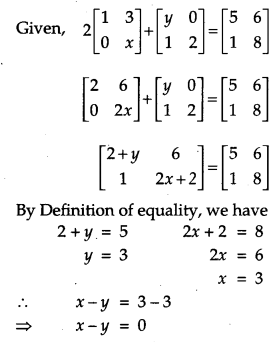
Section – B
Question 6.
If A = \(\left[\begin{array}{ccc}{2} & {0} & {1} \\ {2} & {1} & {3} \\ {1} & {-1} & {0}\end{array}\right]\), then find (A
2
– 5A). [1]
Solution:

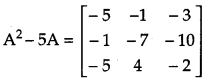
Question 12.
Find: \(\int \frac{\tan ^{2} x \sec ^{2} x}{1-\tan ^{6} x} d x\). [1]
Solution:
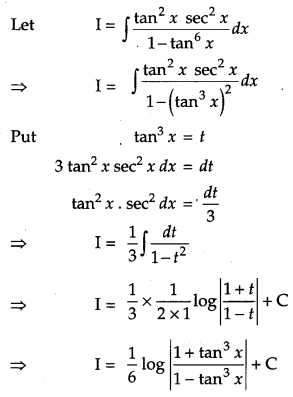
Section – C
Question 13.
Solve for x: tan
-1
(2x) + tan
-1
(3x) = \(\frac{\pi}{4}\). [2]
Solution:
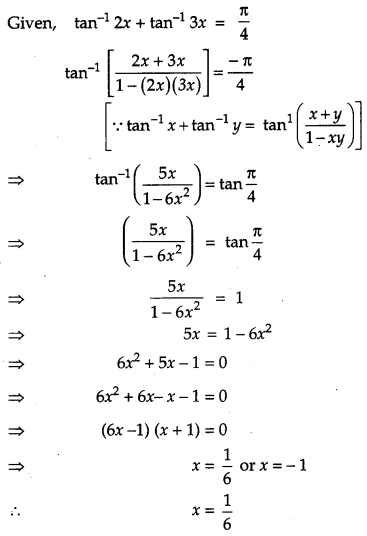
Question 18.
Using properties of determinants, prove the following: [4]
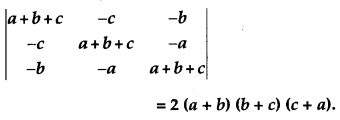
Solution:

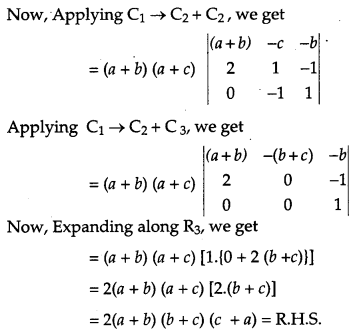
Question 19.
If x = cos t + log tan \(\left(\frac{t}{2}\right)\), y = sin t, then find the values of \(\frac{d^{2} y}{d t^{2}} \text { and } \frac{d^{2} y}{d x^{2}} \text { at } t=\frac{\pi}{4}\). [4]
Solution:
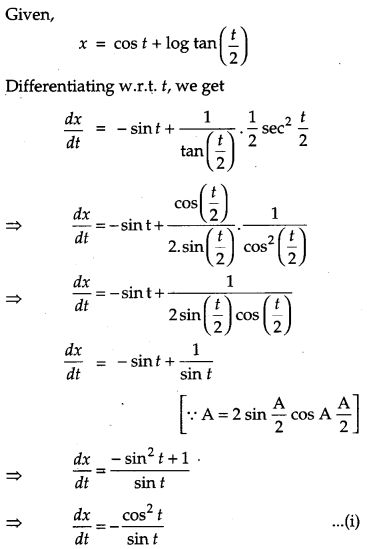
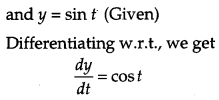
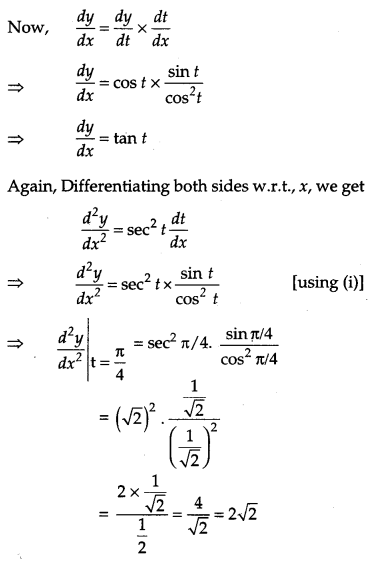
Section – D
Question 24.
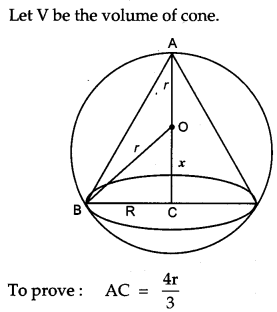
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of a radius r is \(\frac{4 r}{3}\). Also find the maximum volume of cone. 3 [6]
Solution:
Let R be the radius of cone. Let OA = OB = r (radius of sphere)
AC = r + x …(i) (height of cone)
Let V be the volume of cone.

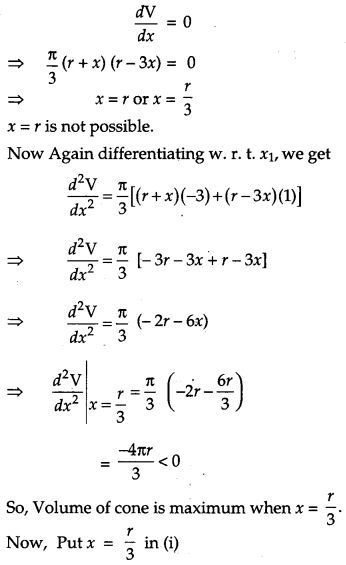

Question 25.
If A = \(\left[\begin{array}{ccc}{2} & {-3} & {5} \\ {3} & {2} & {-4} \\ {1} & {1} & {-2}\end{array}\right]\), then find A
-1
. Hence solve the following system of equations : 2x – 3y + 5z = 11, 3x + 2y – 4z = – 5, x + y – 2z = – 3. [6]
Solution:

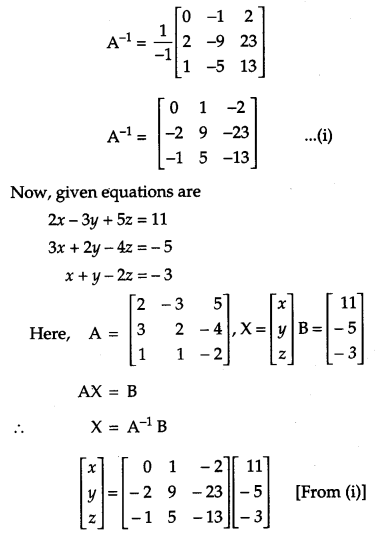
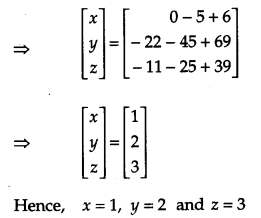
OR
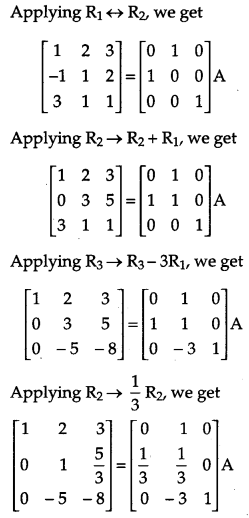
Obtain the inverse of the following matrix using elementary operations:
A = \(\left[\begin{array}{rrr}{-1} & {1} & {2} \\ {1} & {2} & {3} \\ {3} & {1} & {1}\end{array}\right]\)
Solution:
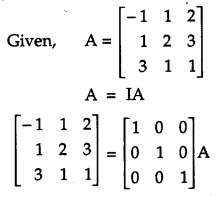
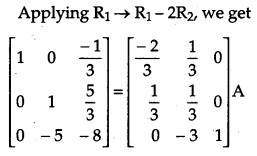
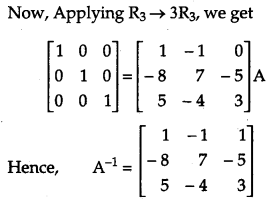
CBSE Previous Year Question Papers Class 12 Maths 2019 Delhi Set III
Note : Except for the following questions, all the remaining questions have been asked in previous sets
Section – A
Question 1.
If 3A – B = \(\left[\begin{array}{ll}{5} & {0} \\ {1} & {1}\end{array}\right]\) and B = \(\left[\begin{array}{ll}{4} & {3} \\ {2} & {5}\end{array}\right]\), then find the matrix A. [1]
Solution:
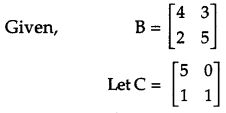
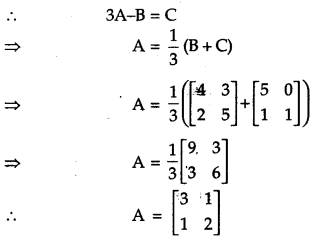
Question 2.
Write the order and the degree of the following differential equation: [1]
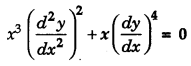
Solution:
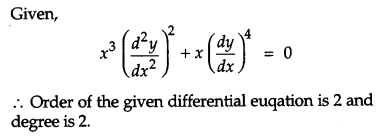
Section – B
Question 5.
Find: \(\int \sin x \cdot \log \cos x d x\) [2]
Solution:
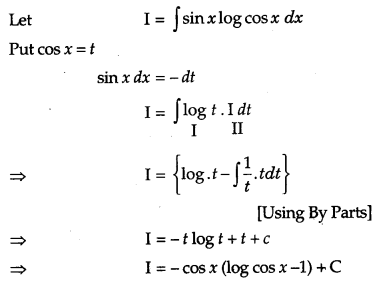
Question 6.
Evaluate : \(\int_{-\pi}^{\pi}\left(1-x^{2}\right) \sin x \cos ^{2} x d x\). [2]
Solution:
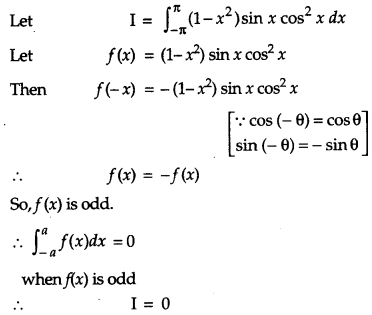
OR
Evaluate: \(\int_{-1}^{2} \frac{|x|}{x} d x\).
Solution:
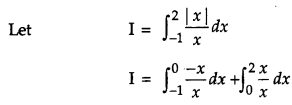
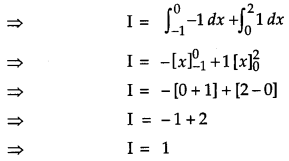
Question 8.
Find a matrix A such that 2A – 3B + 5C = 0, where [2]
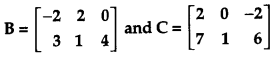
Solution:
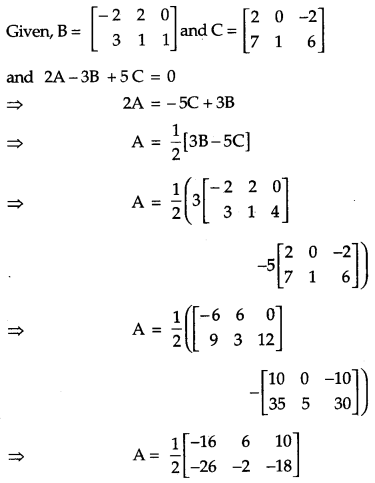
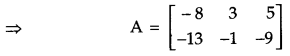
Section – C
Question 13.
Using propeties of determinants, prove the following: [4]
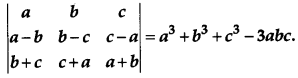
Solution:
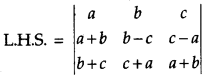

Hence Proved.
Question 20.
Find: \(\int \frac{\cos x}{(1+\sin x)(2+\sin x)} d x\) [4]
Solution:

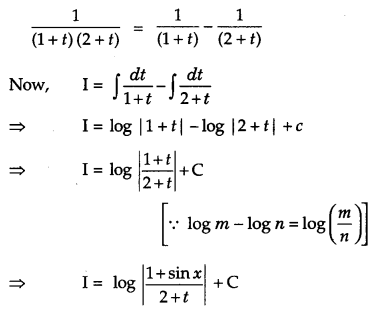
Question 21.
Solve the differential equation: [4]
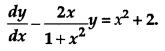
Solution:
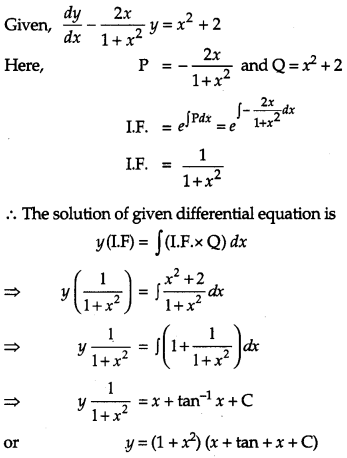
OR
Solve the differential equation: [4]
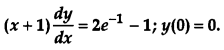
Solution:
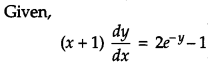
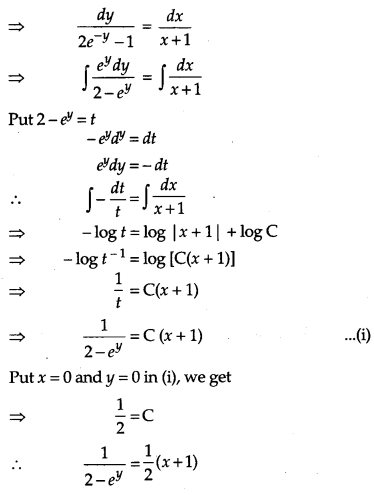
Section – D
Question 26.
Prove that the curves y
2
= 4x and x
2
= 4y divide the by of the squre bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts. [6]
Solution:
Given, y
2
= 4x …(i)
x
2
= 4y …(ii)
x = 0, x = y, y = 0 and y = 4
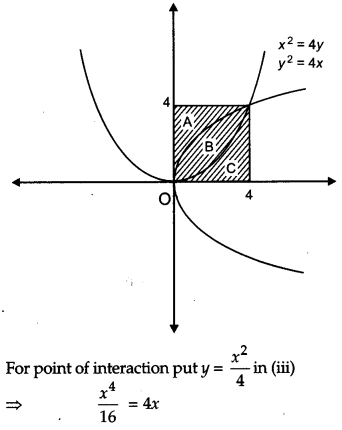


The curves y
2
= 4x and x
2
= 4y divides the area of the square into three equal parts. Hence Proved.
OR
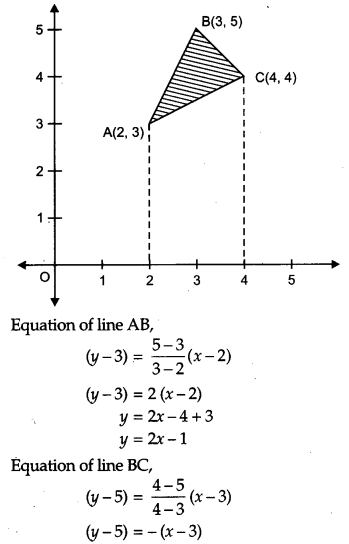
Using integration, find the area of the triangle whose vertices are (2, 3), (3, 5) and (4, 4).
Solution:
Given, the vertices of AABC, A(2, 3), B (3, 5) and C (4, 4).
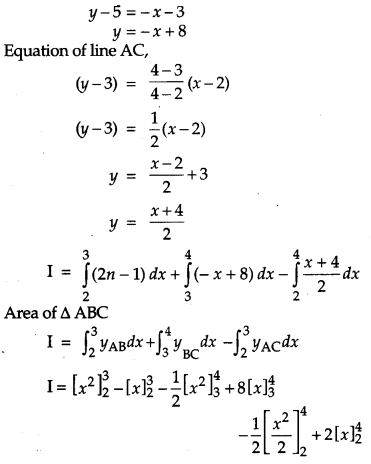
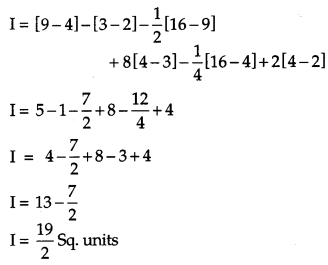
Question 29.
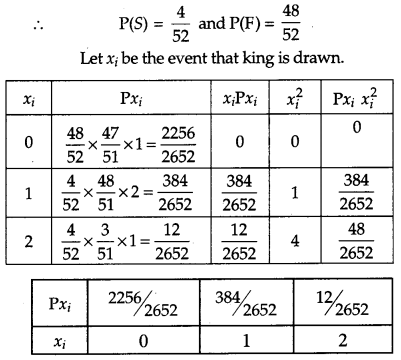
Two cards are drawn simultaneously (or successively without replacement) from a well shuffled pack of 52 cards. Find the mean and variance of the number of kings. [4]
Solution:
Let S = Number of kings.
and F = number of non kings