CBSE Previous Year Question Papers Class 12 Maths 2012 Outside Delhi
Time allowed: 3 hours
Maximum marks : 100
General Instructions:
- All questions are compulsory.
- The question paper consists of 29 questions divided into four sections A, B, C and D. Section A comprises of 4 questions of one mark each, Section B comprises of 8 questions of two marks each, Section C comprises of 11 questions of four marks each and Section D comprises of 6 questions of six marks each.
- All questions in Section A are to be answered in one word, one sentence or as per the exact requirement of the question.
- There is no overall choice. However, internal choice has been provided in 1 question of Section A, 3 questions of Section B, 3 questions of Section C and 3 questions of Section D. You have to attempt only one of the alternatives in all such questions.
- Use of calculators is not permitted. You may ask for logarithmic tables, if required.
**Answer is not given due to the change in present syllabus
CBSE Previous Year Question Papers Class 12 Maths 2012 Outside Delhi Set I
Section -A
Question 1.
The binary operation *: R × R → R is defined as a * b = 2a + b. Find (2 * 3) * 4.** [1]
Question 2.
Find the principal value of tan
-1
\( \sqrt{{3}} \) – sec
-1
(-2) [1]
Solution:
tan
-1
\( \sqrt{{3}} \) – sec
-1
(-2) …(i)
We know that the range of principal value of
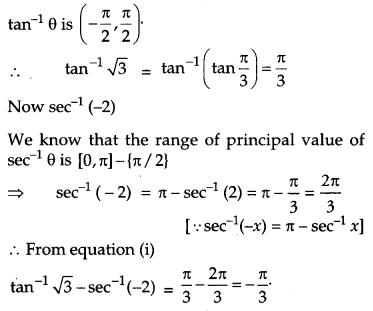
Question 3.
Find the value of x+y from the following equation:
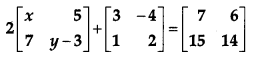 [1]
[1]
Solution:
Given that,
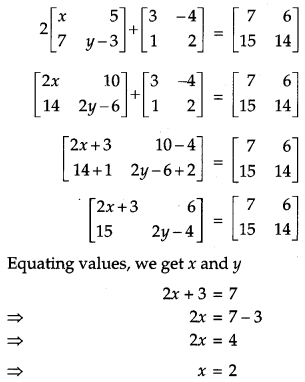
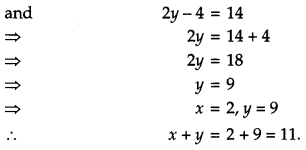
Question 4.
If A
T
= \(\left[\begin{array}{rr}{3} & {4} \\ {-1} & {2} \\ {0} & {1}\end{array}\right]\) and B = \(\left[\begin{array}{rrr}{-1} & {2} & {1} \\ {1} & {2} & {3}\end{array}\right]\), then find A
T
= B
T
. [1]
Solution:
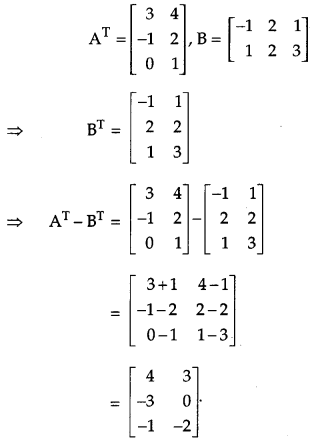
Question 5.
Let A ba a square matrix of order 3 × 3. Write the value of |2A|, where |A| = 4. [1]
Solution:
In a square matrix of order 3 × 3,
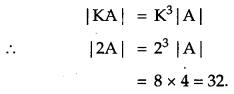
Question 6.
Evaluate:
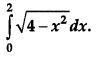 [1]
[1]
Solution:
We know that,
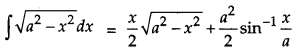
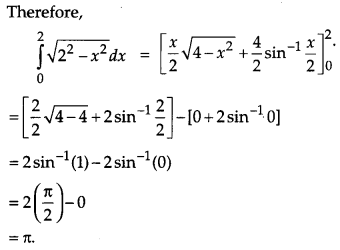
Question 7.
Given \(\int e^{x}(\tan x+1) \sec x d x=e^{x} f(x)+c\). Write f(x) satisfying the above. [1]
Solution:
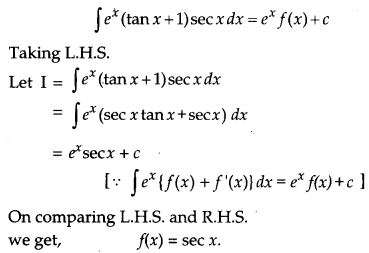
Question 8.
Write the value of \((\hat{i} \times \hat{j}) \cdot \hat{k}+\hat{i} \cdot \hat{j}\) [1]
Solution:
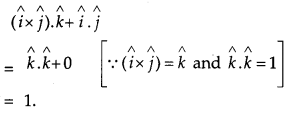
Question 9.
Find the scalar components of the vector \(\overrightarrow{\mathbf{A B}}\) with initial point A (2, 1) and terminal point B (- 5, 7). [1]
Solution:
Position vector of A

Question 10.
Find the distance of the plane 3x – 4y + 12z = 3 from the origin. [1]
Solution:
We know that the distance of the point (x
1
, y
1
, z
1
) from the plane ax + by + cz + d = 0 is
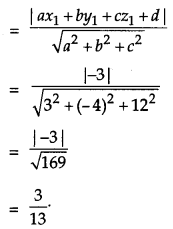
Section – B
Question 11.
Prove the following:
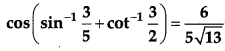 [4]
[4]
Solution:
Taking L. H. S
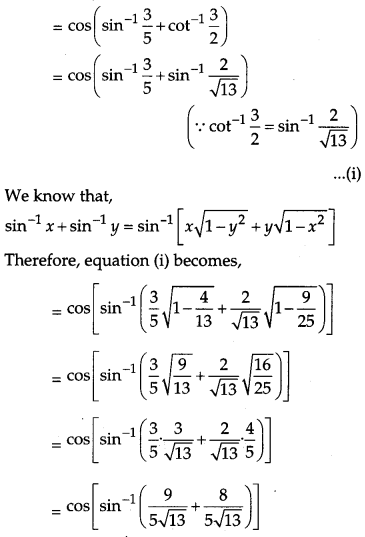
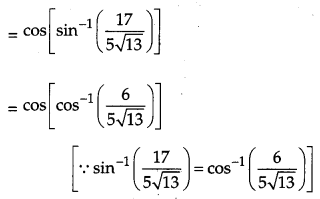

Question 12.
Using properties of determinants, show that
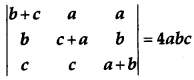 [4]
[4]
Solution:

Question 13.
Show that f : N → N, given by
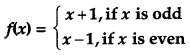
is both one-one and onto. [4]
Solution:
Let x, y ϵ R such that f(x) = f(y)
m=m
If x and y are odd, then
∴ f(x) = f(y)
⇒ x + 1 = y + 1
⇒ x = y
If x and y are even, then
f(x) = f(y)
⇒ x – 1 = y – 1
⇒ x = y
f(x) = x + 1 is even and f(y) = y + 1 is odd.
∴ x ≠ y ⇒ f(x) ≠ f(y)
Similarly if x is even and y is odd, then
x ≠ y ⇒ f(x) ≠ f(y)
Hence, f : N → N is one-one .
Also, f(1) = 1 + 1 = 2
f(1) = 2 (∵ is odd)
If x is odd number, then 3 an even natural number, x + 1 ϵ N such that,
f(x + 1) = x + 1 – 1
= x
If x is even number, then there exist a odd natural number x – 1 ϵ N such that,
f(x – 1) = x – 1 + 1
= x
Hence for every y ϵ N Ǝ x ϵ N such that f(x) = y,
so f is onto.
Hence f is both one-one and onto.
Hence Proved.
OR
Consider the binary operations * : R × R → R and o : R × R→R defined as a*b= | a-b | and aob=a for all a, b ϵ R. Show that is commutative but not associative, ‘o’ is associative but not commutative.**
Question 14.
If x= \(x=\sqrt{a^{\sin ^{-1} t}}, y=\sqrt{a^{\cos ^{-1} t}}, \text { show that } \frac{d y}{d x}=-\frac{y}{x}\). [4]
Solution:
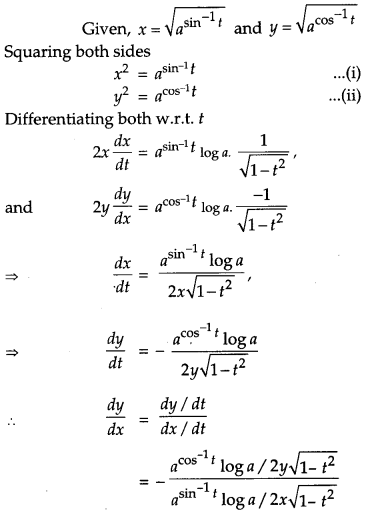

OR
Differentiate \(\tan ^{-1}\left[\frac{\sqrt{1+x^{2}}-1}{x}\right]\) with respect to x.
Solution:
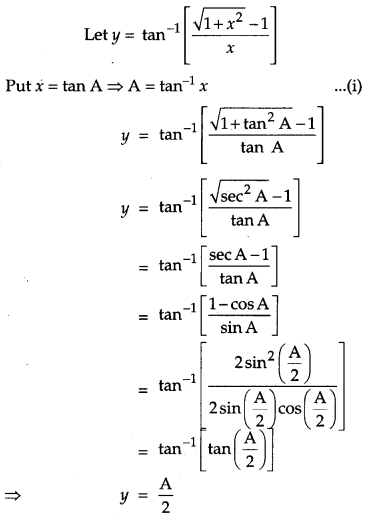
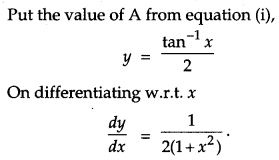
Question 15.
If x = a(cos t + t sin t) and y = a(sin t – t cos t), 0 < t < \(\frac{\pi}{2}\), find \(\frac{d^{2} x}{d t^{2}}, \frac{d^{2} y}{d t^{2}} \text { and } \frac{d^{2} y}{d x^{2}}\). [4]
Solution:
Given, x = a(cos t + t sin t)
On differentiating w.r.t. t, we get
![]()

Question 16.
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall ? [4]
Solution:
Let AC = 5 m be the ladder and y be the height of the wall at which the ladder touches. Also, let the foot of the ladder be at C whose distance from the wall is x m

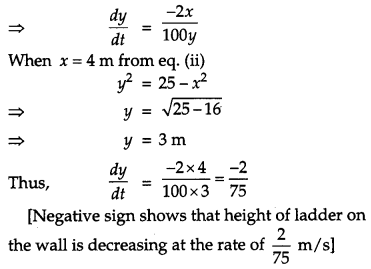
Question 17.
Evaluate: [4]
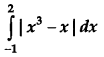
Solution:
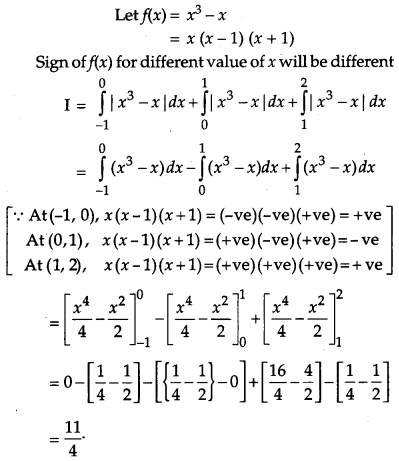
OR
Evaluate:
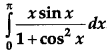
Solution:
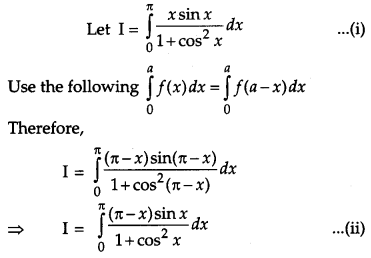
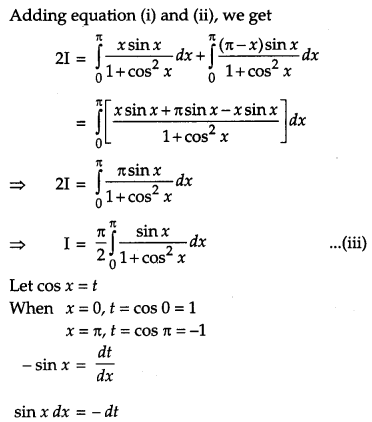
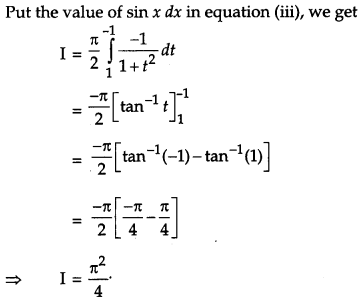
Question 18.
Form the differential equation of the family of circles in the second quadrant and touching the coordinate axes. [4]
Solution:
The equation of circle in second quadrant which touches the coordinate axis is
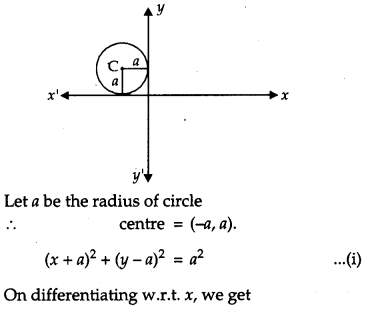

OR
Find the particular solution of the differential equation x(x
2
– 1)\(\frac{d y}{d x}\) = 1; y = 0 when x = 2.
Solution:
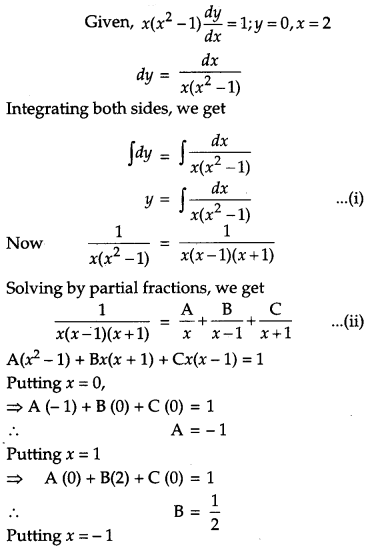
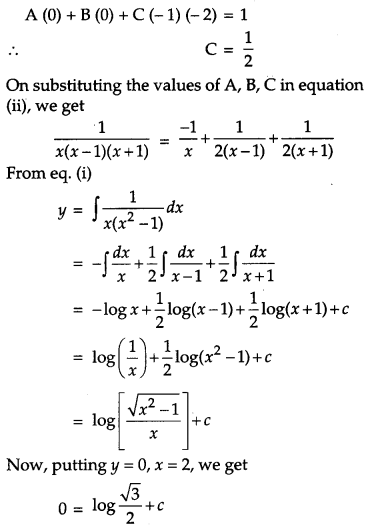
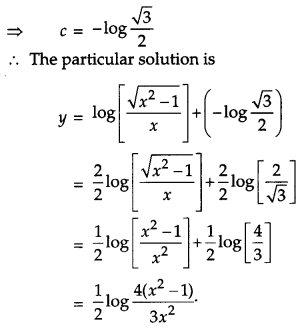
Question 19.
Solve the following differential equation :
(1 + x
2
) dy + 2xy dx = cot x dx; x ≠ 0. [4]
Solution:
(1 + x
2
) dy + 2xy dx = cot x dx
Dividing with (1 + x
2
) dx on both sides, we get
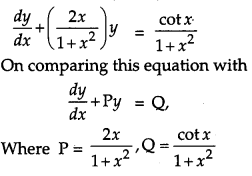
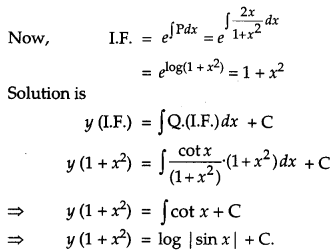
Question 20.
Let \(\vec{a}=\hat{i}+4 \hat{j}+2 \hat{k}, \vec{b}=3 \hat{i}-2 \hat{j}+7 \hat{k} \text { and } \vec{c}=2 \hat{i}-\hat{j}+4 \hat{k}\) Find a vector \(\vec{p}\) which is perpendicular to both \(\vec{a} \text { and } \vec{b}\) and \(\vec{p} \cdot \vec{c}\) = 18. [4]
Solution:
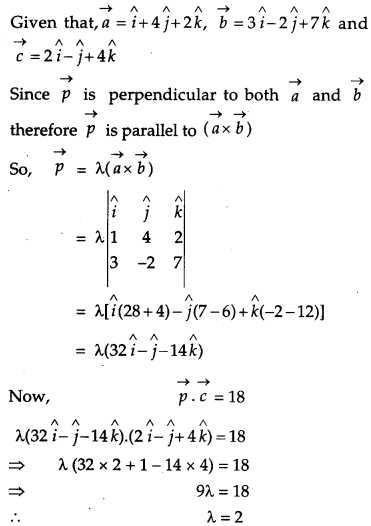
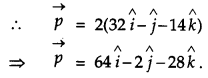
Question 21.
Find the coordinates of the point where the line through the points A = (3, 4, 1) and B = (5, 1, 6) crosses the XY-plane. [4]
Solution:
Given, A = (3, 4, 1), B = (5, 1, 6)
The equation of the line passing through above
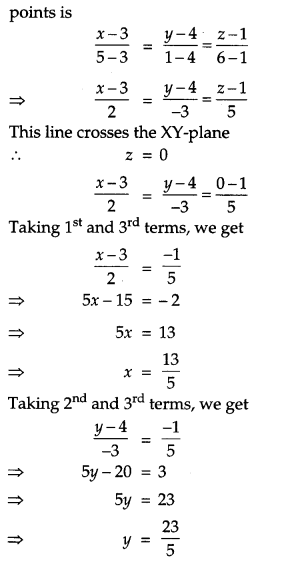

Question 22.
Two cards are drawn simultaneously (without replacement) from a well-shuffled pack of 52 cards. Find the mean and variance of the number of red cards. [4]
Solution:
Let P (A) = Probability of getting one red card.
Number of red cards = 26
Let X be the random variable which can take values 0, 1, 2 where X is the number of red cards selected

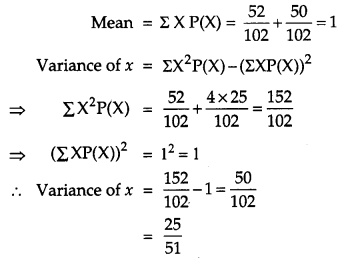
Section – C
Question 23.
Using matrices, solve the following system of equations:
2x + 3y + 3z = 5, x – 2y + z = – 4, 3x – y – 2z = 3. [6]
Solution:
Given, 2x + 3y + 3z = 5,
x – 2y + z = – 4,
3x – y – 2z = 3
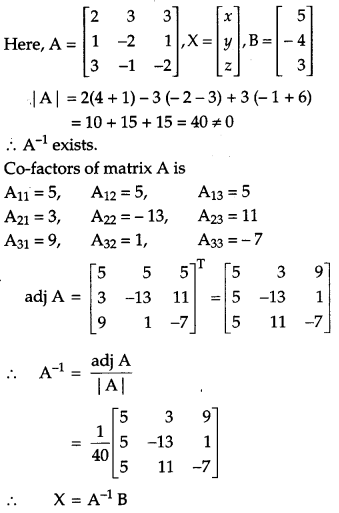
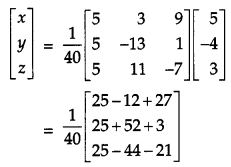
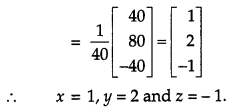
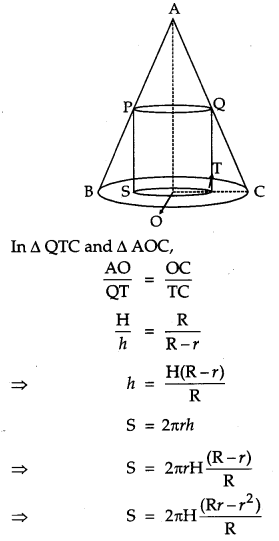
Question 24.
Prove that the radius of the right circular cylinder of greatest curved surface area which can be inscribed in a given cone is half of that of the
cone. [6]
Solution:
Let r = radius of cylinder
R = radius of cone
h = height of cylinder
H = height of cone
Curved surface area of cylinder = 2πrh

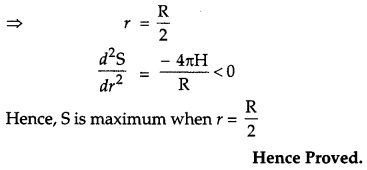
OR
An open box with a square base is to be made out of a given quantity of cardboard of area c
2
square units. Show that the maximum volume of the box is \(\frac{c^{3}}{6 \sqrt{3}}\) cubic units.
Solution:
Let l = x, b = x, h = y
∴ Area of open box = Area of cardboard

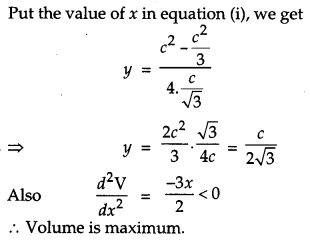
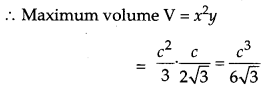
Question 25.
Evaluate: [6]
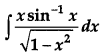
Solution:

OR
Evaluate:
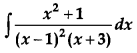
Solution:
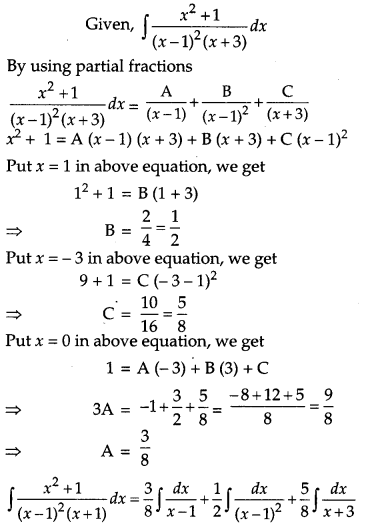
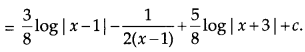
Question 26.
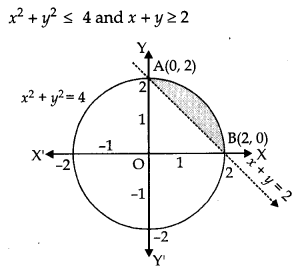
Find the area of the region {(x, y) : x
2
+ y
2
≤ 4, x + y ≥ 2}. [6]
Solution:
We have two equations

Question 27.
If the lines \(\frac{x-1}{-3}=\frac{y-2}{-2 k}=\frac{z-3}{2} \text { and } \frac{x-1}{k}=\frac{y-2}{1}\) \(=\frac{z-3}{5}\) are perpendicular, find the value of k and hence find the equation of plane containing these lines. [6]
Solution:
The equation of the given lines are
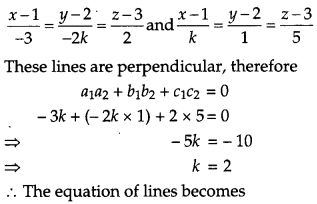
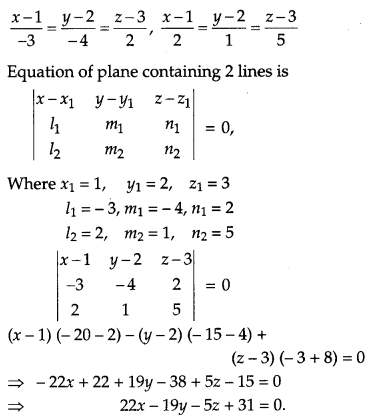
Question 28.
Suppose a girl throws a die. If she gets a 5 or 6, she tosses a coin 3 times and notes the number of heads. If she gets 1, 2, 3 or 4 she tosses a coin once and notes whether a head or tail is obtained. If she obtained exactly one head, what is the probability that she threw 1, 2, 3 or 4 with the die? [6]
Solution:
The outcome of an experiment can be represented as
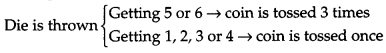
If she gets 1, 2, 3 or 4, sample space will be (1H), (2H), (3H), (4H), (1T), (2T), (3T), (4T)
If she gets 5 or 6, sample space will be
(5 HHH), (5 HTT), (5 HHT), (5 HTH), (5 THT), (5 TTH), (5 THH), (5 TTT), (6 HHH), (6 HTT), (6 HHT), (6 HTH), (6 THT), (6 TTH), (6 THH), (6 TTT)
Let
A = Getting 1, 2, 3 or 4 on die
B = Getting exactly 1 Head
A = (1H), (2H), (3H), (4H), (1T), (2T), (3T), (4T)
B = (1H), (2H), (3H), (4H), (5HTT), (5THT), (5TTH), (6HTT), (6TTH), (6THT)


Question 29.
A dietician wishes to mix two types of foods in such a way that the vitamin contents of the mixture contains at least 8 units of vitamin A and 10 units of vitamin C. Food I contains 2 units/kg of vitamin A and 1 unit/kg of vitamin C while food II contains 1 unit/kg of vitamin A and 2 units/kg of vitamin 1 unit/kg of vitamin C. It costs ₹ 5 per kg to purchase food I and ₹ 7 per kg to purchase Food II. Determine the minimum cost of such a mixture. Formulate the above as a LPP and solve it graphically. [6]
Solution:
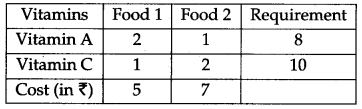
Let the amount of food I = x kg
Let the amount of food II = y kg
If Z denotes the total cost
To minimize the cost we have to minimize Z.
Subject to the constraints,
2x + y ≥ 8
x + 2y ≥ 10
x ≥ 0
y ≥ 0
Minimize Z = 5x + 7y
First we draw the lines AB and CD whose equations are
2x + y = 8 ..(ii)
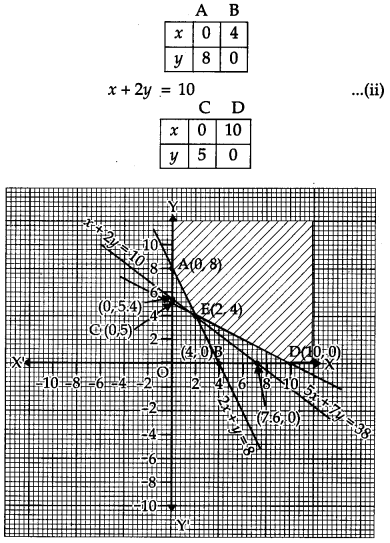
The feasible region is shaded in the figure. The lines are intersecting at the point E (2, 4).
∴ The vertices of the feasible region are A (0, 8), E (2, 4) and D (10, 0).
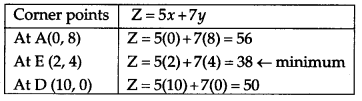
Since the feasible region is unbounded 38 may or may not be minimum value of total cost for this we draw graph of inequality.
5x + 7y < 38

Clearly graph of L has no common point with the feasible region.
∴ The minimum value of Z is 38 at the point E (2, 4). Hence, the amount of food I is 2 kg and amount of food II is 4 kg should be included in the mixture for minimum cost of ₹ 38.
CBSE Previous Year Question Papers Class 12 Maths 2012 Outside Delhi Set II
Note: Except for the following questions, all the remaining questions have been asked in previous set.
Section – A
Question 10.
Write the value of \(\hat{(k \times \hat{j})} \cdot \hat{i}+\hat{j} \cdot \hat{k}\) [1]
Solution:
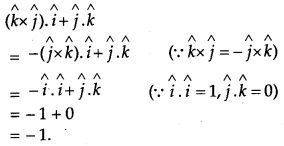
Section – B
Question 19.
Prove the following:
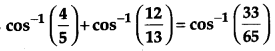 [4]
[4]
Solution:

Question 20.
If y = (tan
-1
x)
2
, show that
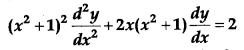 [4]
[4]
Solution:
Given. y = (tan
-1
x)
2
Differentiating w.r.t. x, we get
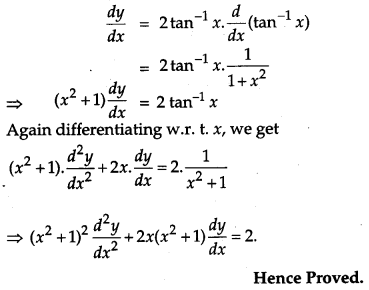
Question 21.
Find the particular solution of the differential equation \(\frac{d y}{d x}\) + y cot x = 4x cosec x, (x ≠ 0), given that y = 0 when x = \(\frac{\pi}{2}\) [4]
Solution:
Given;

This is the required particular solution of the given differential equation.
Question 22.
Find the coordinates of the point where the line through the point (3, -4, -5) and (2, – 3, 1) crosses the plane 2x + y + z = 7. [4]
Solution:
Equation of the line passes through the points (3, -4, -5) and (2, – 3, 1) is
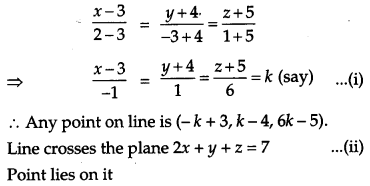
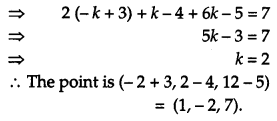
Section – C
Question 28.
Using matrices, solve the following system of equations:
x + y – z = 3; 2x + 3y + z = 10; 3x – y -7z = 1 [6]
Solution:
The given system of equations are
x + y – z = 3;
2x + 3y + z = 10;
3x – y – 7z = 1.
These equations can be written in matrix form
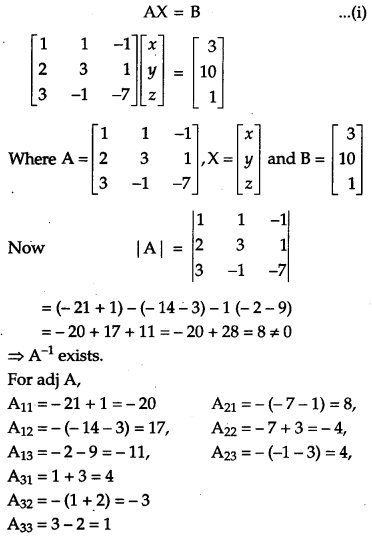
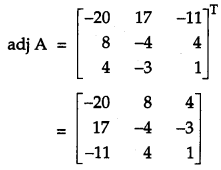

Question 29.
Find the length and the foot of the perpendicular from the point P (7, 14, 5) to the plane 2x + 4y – z = 2. Also find the image of point P in the plane. [6]
Solution:
The given plane is
2x + 4y – z = 2 …(i)
The d.r.s. of the normal to (i) are 2, 4, -1.
∴ Equation of a line perpendicular to (i) passing through P(7, 14, 5) is

which is the length of the perpendicular from P on(i)
Again let R(x, y, z) be the image of P in the plane
(i). Then Q is the mid-point of PR.
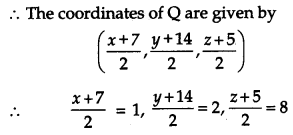
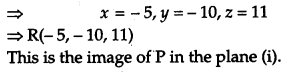
CBSE Previous Year Question Papers Class 12 Maths 2012 Outside Delhi Set III
Note: Except for the following questions, all the remaining questions have been asked in previous sets.
Section – A
Question 9.
Write the value of \((\hat{k} \times \hat{i}) \cdot \hat{j}+\hat{i} \cdot \hat{k}\) [1]
Solution:
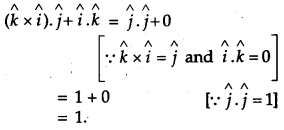
Question 10.
Find the value of x + y from the following equations:
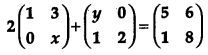 [1]
[1]
Solution:
Given,
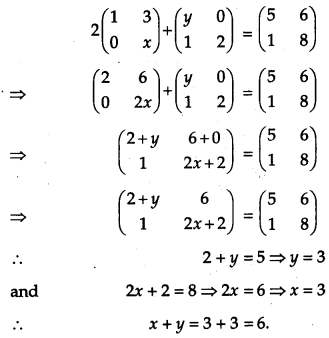
Section – B
Question 19.
If x = a(cos t + log tan\(\frac{t}{2}\)), y = a sin t, find \(\frac{d^{2} y}{d t^{2}}\) and \(\frac{d^{2} y}{d x^{2}}\) [4]
Solution:
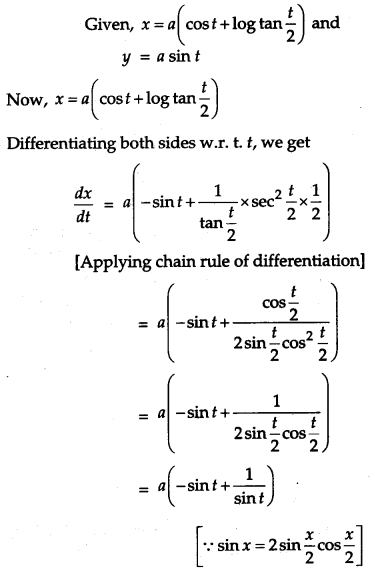


Question 20.
Find the coordinates of the point where the line through the points (3, -4, -5) and (2, – 3, 1) crosses the plane 3x + 2y + z + 14 = 0. [4]
Solution:
The equation of the straight line passing through the points (3, -4, -5) and (2, – 3, 1) is
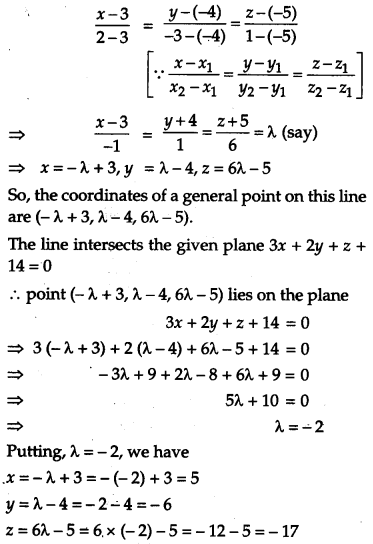
Thus, the point of intersection of the line and the given plane is (5, – 6, -17).
Question 21.
Find the particular solution of the differential equation \(x \frac{d y}{d x}-y+x \sin \left(\frac{y}{x}\right)=0\), given that when x = 2, y = π. [4]
Solution:
Given differential equation is:
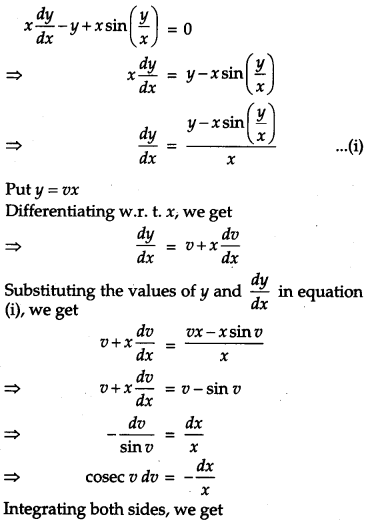
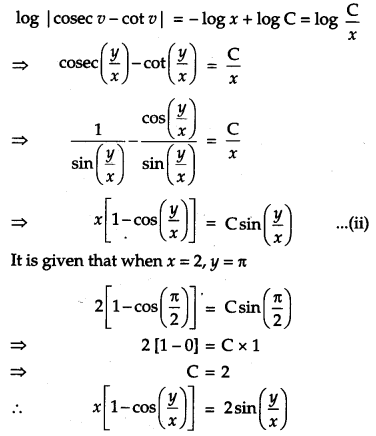
This is the required particular solution of the given differential equation.
Question 22.
Prove the following:
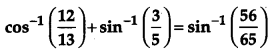 [4]
[4]
Solution:
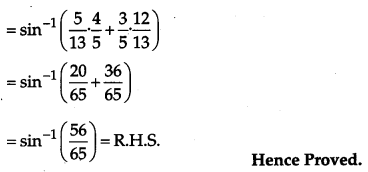
Taking L. H. S
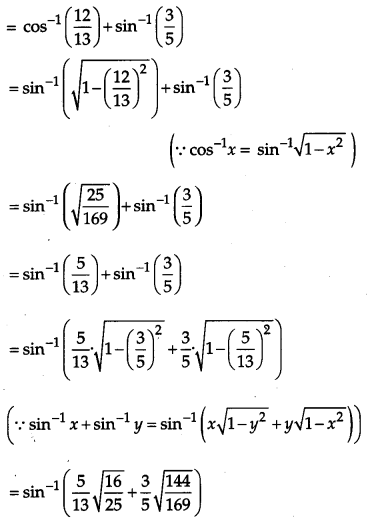
Section – C
Question 28.
Find the coordinates of the foot of perpendicular and the length of the perpendicular drawn from the point P (5, 4, 2) to the line \(\vec{r}=-\hat{i}+3 \hat{j}+\hat{k}+\)\(\lambda(2 \hat{i}+3 \hat{j}-\hat{k})\). Also find the image of Pin this line. [6]
Solution:
The given point is (5, 4, 2) and the given
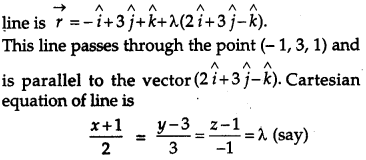


Question 29.
Using matrices, solve the following system of equations:
3x + 4y + 7z = 4;
2x – y + 3z = -3;
x + 2y – 3z = 8
The above system of equations can be represented as AX = B
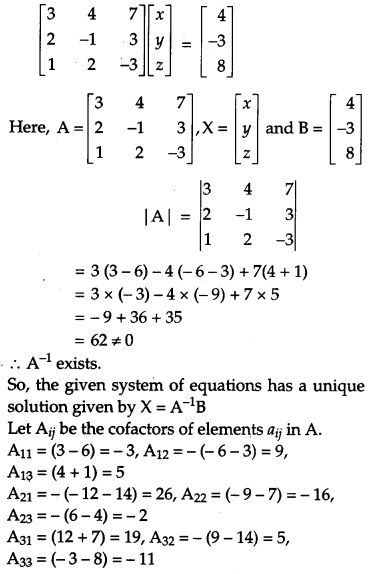
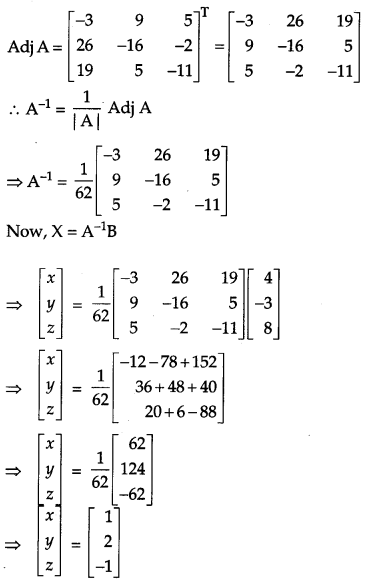
Hence, x = 1, y = 2, z = -1 is the required solution.