CBSE Class 12 Physics Question Paper 2019 (Series: BVM/4) with Solutions

Students can use CBSE Previous Year Question Papers Class 12 Physics with Solutions and CBSE Class 12 Physics Question Paper 2023 (Series: BVM/4) to familiarize themselves with the exam format and marking scheme.

CBSE Class 12 Physics Question Paper 2019 (Series: BVM/4) with Solutions

General Instructions:

Read the following instructions very carefully and follow them:

1. This question paper contains 35 questions. All questions are compulsory.
2. Question paper is divided into FIVE sections – Section A, B, C, D and E.
3. In Section-A: question number 1 to 18 are Multiple Choice (MCQ) type questions carrying 1 mark each.
4. In Section-B: question number 19 to 25 are Short Answer-1 (SA-1) type questions carrying 2 marks each.
5. In Section-C: question number 26 to 30 are Short Answer-2 (SA-2) type questions carrying 3 marks each.
6. In Section-D: question number 31 to 33 are Long Answer (LA) type questions carrying 5 marks each.
7. In Section-E: question number 34 and 35 are case-based questions carrying 4 marks each.
8. There is no overall choice. However, an internal choice has been provided in 2 questions in Section-B, 2 questions in Section-C, 3 questions in Section-D and 2 questions in Section-E.
9. Use of calculators is NOT allowed.
   c = 3 × 10 ⁸ m/s; h = 6.63 × 10 ^-34 Js
   e = 1.6 × 10 ^-19 ; µ ₀ = 4π × 10 ^-7 T m A ^-1
   \(\varepsilon_0\) = 8.854 × 10 ^-12 C ² N ^-1 m ^-2
   \(\frac{1}{4 \pi \varepsilon_0}\) = 9 × 10 ⁹ N m ² C ^-2
   Mass of electron (m _e ) = 9.1 × 10 ^-31 kg; Mass of neutron = 1.675 × 10 ^-27 kg
   Mass of proton = 1.673 × 10 ^-27 kg; Avogadro’s number = 6.023 × 1o ²³ per gram mole
   Boltzmann constant = 1.38 × 10 ^-23 JK ^-1

Code No. 55/4/1
Section A

Question 1.
Two identical conducting balls A and B have charges -Q and +3Q respectively. They are brought in contact with each other and then separated by a distance d apart. Find the nature of the Coulomb force between them. [1]
Or
A metallic spherical shell has an inner radius R ₁ and outer radius R ₂ . A charge Q is placed at the centre of the shell. What will be the surface charge density on the (i) inner surface, and outer surface of the shell?
Answer:
The nature of the coulomb force is REPULSIVE
Or
(i) Surface charge density on inner surface = –\(\frac{Q}{4 \pi R_1^2}\)
(ii) Surface charge density on outer surface = +\(\frac{Q}{4 \pi R_2^2}\)

Question 2.
Under what condition will the current in a wire be the same when connected in series and in parallel of n identical cells each having internal resistance r and external resistance R? [1]
Answer:
Given : emf of each cell = E, internal resistance = r, External Resistance = R

Given:I ₁ = I ₂
\(\frac{n \mathrm{E}}{(n r+\mathrm{R})}\) = \(\frac{\mathrm{E}}{\left(\frac{r}{n}+\mathrm{R}\right)}\)
On solving, (nr + R) = (r + nR); It is the required condition.

Question 3.
The small ozone layer on top of the stratosphere is crucial for human survival. Why? [1]
Or,
Illustrate by giving suitable examples, ho*v you can show thdt electromagnetic waves carry both energy and momentum.
Answer:
The small ozone layer on top of the atmosphere is crucial for human survival, because ozone layer absorbs the ultra-violet (UV) radiations.
Or
When electromagnetic waves fall on charged particles, they set the charges into motion. This illustrates that em waves carry both-energy and momentum.
Example: Photo-electric Effect.

Question 4.
The figure shows the variation of stopping potential V ₀ with the frequency v of the incident radiations for two photosensitive metals P and Q. Which metal has smaller threshold wavelength? Justify your answer. [1]

Answer:
Metal Q has smaller threshold wavelength, because it has higher frequency of incident radiations
λ = \(\frac{c}{v}\) or λ = \(\frac{1}{v}\)

Question 5.
When electrons drift in a metal from lower to higher potential, does it mean that all the free electrons of the metal are moving in the same direction? [1]
Answer:
No, only the drift velocities of the electrons are superposed over their random (haphazard) thermal velocities. The solid line shows the random path followed by a free electron in the absence of an external field. The electron proceeds from A to B, making six collisions on its path. The dotted curve shows how the random motion of the same electron gets modified when an electric field is applied.

Section B

Question 6.
Apply Gauss’s law to show that for a charged spherical shell, the electric field outside the shell is, as if the entire charge were concentrated at the centre. [2]
Or,
Two large parallel plane sheets have uniform charge densities +a and -a. Determine the electric field (z) between the sheets, and (it) outside the sheets.
Answer:
Electric Field outside charged spherical shell Flux through the small section of Gaussian surface
ϕ = \(\oint \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d s}\)
ϕ = \(\oint \mathrm{E} \cdot d s \cos \theta\)
E || \(d \overrightarrow{s}\), θ = 0
ϕ = E.4πR² ………..(i)
Img
Applying Gauss’s theorem, ϕ = \(\frac{q}{\varepsilon_0}\) ……………(ii)

From equations (i) and (ii), E = \(\frac{1}{4 \pi \varepsilon_0}\) • \(\frac{q}{R^2}\)

The expression indicates that the entire charge was concentrated at the centre.

Or,

Now’ electric field intensity due to a plane sheet of charge is given by E = \(\frac{+\sigma}{2 \varepsilon_0}\)
Here E = \(\frac{+\sigma}{2 \varepsilon_0}\) and E = \(\frac{-\sigma}{2 \varepsilon_0}\)

(i) Electric field at point Q (In between the sheets)
\(\overrightarrow{\mathrm{E}}\) = \(\overrightarrow{\mathrm{E}_{\mathrm{A}}}\) + \(\overrightarrow{\mathrm{E}_{\mathrm{B}}}\)
= \(\frac{\sigma}{2 \varepsilon_0}\) + \(\frac{+\sigma}{2 \varepsilon_0}\) = \(\frac{+\sigma}{\varepsilon_0}\)

(ii) Field at the point P or R (outside the sheets)
\(\overrightarrow{\mathrm{E}}\) = \(\overrightarrow{\mathrm{E}_{\mathrm{A}}}\) + \(\overrightarrow{\mathrm{E}_{\mathrm{B}}}\)
= \(\frac{\sigma}{2 \varepsilon_0}\) + \(\frac{+\sigma}{2 \varepsilon_0}\) = \(\frac{+\sigma}{\varepsilon_0}\)

Question 7.
A long straight wire AB carries a current of 4A. A proton P travels at 4 × 10 ⁶ ms ^-1 parallel to the wire 0.2 m from it and in a direction opposite to the current as shown in the figure. Calculate the force which the magnetic field due to the current carrying wire exerts on the proton. Also specify its direction. [2]

Answer:
Given: I = 4A, v = 4 × 10 ⁶ ms ^-1 , r = 0.2 m, q = 1.6 × 10 ^-16 , C.F = ?
Direction of Force = ?
Magnetic filed at Point P due current carrying straight wire AB
B = \(\frac{\mu_0}{2 \pi}\) \(\frac{\mathrm{I}}{r}\)
Force acting on the moving proton in the magnetic field,
F = Bqv sin θ
Therefore F = (\(\frac{\mu_0}{2 \pi}\) \(\frac{\mathrm{I}}{r}\)) × (qv sin θ)

= \(\frac{\left(2 \times 10^{-7}\right) \times 4 \times\left(1.6 \times 10^{-19}\right) \times\left(4 \times 10^6\right) \sin 90^{\circ}}{(0.2)}\)

On solving = 2.56 x 10 ^-18 N
∴ Direction of force at point P is towards the right, (away from AB)

Twinkling

Question 8.
A parallel plate capacitor of plate area ‘A’ each and separation ‘d’, is being charged by an ac source. Show that the displacement current inside the capacitor is the same as the current charging the capacitor. [2]
Answer:
When the capacitor is getting charged, we have

Electric flux = ϕ _E (t) = \(\frac{Q(t)}{\varepsilon_0}\)
Now Q(t) = CV(t) = C(V ₀ sinωt)
ϕ _t = \(\frac{1}{\varepsilon_0}\) CV ₀ sinωt
Displacement current (i _d ) = ε ₀ \(\frac{d \phi_{\mathrm{E}}}{d t}\)
= ε ₀ [latex]\frac{1}{\varepsilon_0} \cdot \frac{d}{d t}\left(\mathrm{CV}_0 \sin \omega t\right)[/latex]
= ωC V ₀ cosωt
= ωC V ₀ sin(ωt + π/2) …………(i)

Also, Conduction current ic leads the voltage by π/2

i _c = \(\frac{V_0}{(1 / \omega C)}\) sin (t + π/2) = CV sin(ωt + π/2)
From equations (i) and (ii) we can conclude that:
i _d = i _d
i.e., displacement current inside the capacitor is the same as the current charging the capacitor.

Question 9.
A beam of light converges at a point P. Now a convex lens is placed in the path of the convergent beam at 15 cm from P. At what point does a beam converge if the convex lens has a focal length 10 cm? [2]
Or,
An object is kept in front of a concave mirror of focal length 15 cm. The image formed is real and three times the size of the object. Calculate the distance of the object from the mirror.
Answer:
Given that a beam of light converges at a point P, as shown in the ray diagram. Now a convex of focal length 10 cm is kept in the path of convergent beam at 15 cm from the point P.

From lens formula, we have \(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\)

Here u = + 15 cm; f = +10 cm
\(\frac{1}{v}\) = \(\frac{1}{f}\) + \(\frac{1}{u}\)
= \(\frac{1}{10}\) + \(\frac{1}{15}\)

Now the beam will converge at a distance of 6 cm from the lens.

Or

Given: m = +3 and f= -15 cm for a concave mirror
∵ m =\(\frac{v}{u}\) 3 ∴ v = 3 u
\(\frac{1}{f}\) = \(\frac{1}{v}\) + \(\frac{1}{u}\)
\(\frac{1}-15}\) = \(\frac{1}{3u}\) + \(\frac{1}{u}\) ⇒ u = 20
The object distance is 20 cm.

Question 10.
Explain giving reason, how the resolving power of a compound microscope depends on the
(a) frequency of the incident light.
(b) focal length of the objective lens. [2]
Answer:
Resolving power of a compound microscope = \(\frac{2 \mu \sin \theta}{1.22 \lambda}\) = \( × [latex]\frac{v}{c}\)
Therefore, it is clear that the resolving power
(a) increases with the frequency of incident light, and
(b) is independent of the focal length of the objective lens.

Question 11.
The figure shows a modified Young’s double slit experimental set-up.
Here SS ₂ – SS ₁ = λ/4.

(a) Write the condition for constructive interference.
(b) Obtain an expression for the fringe width. [2]
Answer:
Given:
SS ₂ – SS ₁ = λ/4.
∴ The path difference S ₂ P – S ₁ P = (\(\frac{y_n d}{D}+\frac{\lambda}{4}\) )

(a) For constructive interference
Path difference = rik where n = 0,1, 2,3..
\(\frac{y_n d}{D}+\frac{\lambda}{4}\) = nX is the condition for constructive interference

(b) Consider two coherent sources S ₁ and S ₂ separated by a distance d. Let D be the distance between the screen and the plane of slits S ₁ and S ₂ .

Light waves emitted from S ₁ and S ₂ reach point O on the screen after travelling equal distances. So path difference and hence phase difference between these waves is zero. Therefore, they meet at O in phase and hence constructive interference takes place at O. Thus O is the position of the central bright fringe.
Expression for the fringe width.
Let d = distance between slits S ₁ and S ₂
D = distance of screen from two slits
x = distance between the central maxima O and observation point P

Light waves spread out from S and fall on both S ₁ and S ₂ . The spherical waves emanating from S ₁ and S ₂ will produce interference fringes on the screen MN.

In rt ∆S ₁ AP, we have
(S ₁ S) ² = (S ₁ A) ² + (AP) ²

Let the waves emitted by S1 and S2 meet at point P and the screen at a distance y from the central bright fringe.
The path difference between these waves at P is given by
∆x = S ₂ P – S ₁ P

Question 12.
(i) State the principle on which the working of an optical fiber is based,
(ii) What are the necessary conditions for this phenomenon to occur?
Answer:
(i) Working of an optical fibre is based on the principle of total internal reflection
(ii) (a) Light should travel from a denser to rarer medium.
(b) Angle of incidence should be more than critical angle given by i _c = sin ^-1 (\(\frac{1}{\mu}\))

Section C

Question 13.
(a) Draw a graph showing the variation of current versus voltage in an electrolyte when an external resistance is also connected.
(b) (i) The graph between resistance (R) and-temperature (T) for Hg is shown in the figure
(a) Explain the behaviour of Hg near 4 K.
(ii) In which region of the graph shown in the figure (b) is the resistance negative and why? [3]

Answer:
(a) Graph for I vs V for an Electrolyte :

(b) (i) At a temperature of 4 K, the resistance of Hg become zero, which implies that it becomes super conductor at temperature of 4K.

Question 14.
(a) Deduce the relation between current I flowing through a conductor and drift velocity V _d of the electrons.
(b) Figure shows a plot of current T flowing through the cross-section of a wire versus the time Y. Use the plot to find the charge flowing in 10s through the wire.
Answer:
(a) Relation between electric current and drift velocity: Consider a uniform metallic wire XY of length l and cross-sectional area A. A potential difference V is applied across the ends X and Y of the wire. This causes an electric field at each point of the wire of strength:

E = \(\frac{V}{l}\) ………….(i)
Due to this electric field, the electrons gain a drift velocity V _d opposite to direction of electric field. If q be the charge passing through the cross-section of wire in t seconds,
then, current in wire, I = \(\frac{q}{t}\)
The distance transversed by each electron in time (t) = drift velocity × time = V _d t
If we consider two planes P and Q at a distance V _d t in a conductor, then the total charge flowing in time t will be equal to the total charge on the electrons present within the cylinder PQ.
The volume of this cylinder = cross sectional area × length = A (V _d t)
If n is the number of free electrons in the wire per unit volume, then the number of free electrons in the cylinder = n(V _d t)
If charge on each electron is -e(e = 1.6 × 10 ^-19 C), then the total charge flowing through a cross-section of the wire,
q = (nV _d t)(-e) = -neA(V _d t) … (iii)
∴ Current flowing in the wire,
I = \(\frac{q}{t}\) = \(\frac{-n e \mathrm{AV}_d t}{t}\)
i.e., Current I = – neA V _d … (iv)
This is the relation between electric current and drift velocity. Negative sign shows that the direction of current is opposite to the drift velocity.

(b) Charge = Current × time

(i) For 0 to 5 seconds, the current = \(\frac{0+5}{2}\) = 2.5 A
Hence, q ₁ = (2.5) × (5) = 12.5 C
(ii) For 5 sec to 10 sec, the current = 5A
Hence, q ₂ = 5 × (10 – 5) = 5 × 5 = 25 C
q = q ₁ + q ₂ = 12.5 + 25 = 37.5 C

Question 15.
A proton, a deuteron and an alpha particle are accelerated through the same potential difference and then subjected to a uniform magnetic field \(\overrightarrow{B}\), perpendicular to the direction of their motions. Compare (i) their kinetic energies, and (ii) if the radius of the circular path described by proton is 5 cm, determine the radii of the paths described by deuteron and alpha particle. [3]
Answer:
(i) Since qV = \(\frac{1}{2}\) mv²

For proton (KE) _p = \(\frac{1}{2}\) m _p v² ₁ = qV

For deuteron (KE) _d = \(\frac{1}{2}\) m _d v² ₂ = qV

For alpha particle (KE) _α = \(\frac{1}{2}\) m _α v² ₃ = 2qV

(KE) _p : (KE) _d : (KE) _α : 1 : 1 : 2

(ii) ∴ BqV = \(\frac{mv^2}{r}\) r = \(\frac{mv}{Bq}\)
Given: r _p = \(\frac{m_p v}{\mathrm{~B} q_p}\) = 5 cm
Accordingly, r _d = \(\frac{m_d v}{\mathrm{~B} q_d}\) = 10 cm

r _α = \(\frac{m_\alpha v}{\mathrm{~B} q_\alpha}\) = 10 cm [∵ m _α = 4 m _α ; q _α = 2q _p ]

Question 16.
(a) Briefly explain how a galvanometer is converted into an ammeter.
(b) A galvanometer coil has a resistance of 15 Ω and it shows full scale deflection for a current of 4 mA. Convert it into an ammeter of range 0 to 6 A. [3]
Or,
(a) Briefly explaixa how a galvanometer is converted into a voltmeter.
(b) A voltmeter of a certain range is constructed by connecting a resistance of 980 Ω in series with a galvanometer. When the resistance of 470 Ω is connected in series, the range gets halved. Find the resistance of the galvanometer.
Answer:
(a) A galvanometer is converted into an ammeter by connecting small resistance called shunt (S) in parallel to coil of the galvanometer.
S = \(\frac{\mathrm{I}_g \mathrm{G}}{\mathrm{I}-\mathrm{I}_g}\)

(b) Given: G = 15 Ω, I _g = 4 × 10 ^-3 A, I = 6 A, S = ?
We have S = \(\frac{\mathrm{I}_g}{\mathrm{I}-\mathrm{I}_g}\) × G
S = \(\frac{\left(4 \times 10^{-3} \times 15\right)}{\left(6-4 \times 10^{-3}\right)}\)
= \(\frac{60 \times 10^{-3}}{(6-0.004)}\)
= \(\frac{60 \times 10^{-3}}{5.996}\)
= 10 × 10 ^-3 = 0.01 Ω

Or,
(a) A galvanometer is converted into voltmeter by connecting a high value resistance R in series with coil of the galvanometer. The value of (R) is related to the maximum voltage (V) to be measured as (R = \(\frac{V}{I_g}\) – G)

(b) Given: R ₁ = 980 Ω, R ₂ = 470 Ω, \(\frac{V_1}{V_2}\) = \(\frac{1}{2}\), R _g = ?

I _g = \(\frac{\mathrm{V}}{\mathrm{R}_g+\mathrm{R}}\)
⇒ \(\frac{\mathrm{V}_1}{\mathrm{R}_g+980}\) = \(\frac{\mathrm{V}_2}{\left(\mathrm{R}_g+470\right)}\) = \(\frac{V_1}{2\left(R_g+470\right)}\)
2R _g + 940 = R _g + 980
∴ R _g = 40 is the resistance of galvanometer.

Question 17.
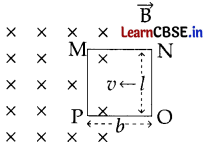
The figure shows a rectangular conducting frame MNOP of resistance R placed partly in a perpendicular magnetic field \(\overrightarrow{B}\) and moved with velocity \(\overrightarrow{v}\) as shown in the figure.

Obtain the expressions for the
(a) force acting on the arm ‘ON’ and its direction, and
(b) power required to move the frame to get a steady emf induced between the arms MN and PO.
Answer:
(a) Given : magnetic field = \(\overrightarrow{B}\) , velocity = \(\overrightarrow{v}\) , length = l, breadth = b, F = ?, Direction =?
The induced emf in the moving conductor MNOP, e = Blv
The induced current, i = \(\frac{e}{R}\) = \(\frac{Blv}{R}\)
Force on the arm ‘ON’, F = Bil = \(\frac{(\mathrm{B}) \times(\mathrm{B} l v) l}{\mathrm{R}}\) = \(\frac{\mathbf{B}^2 l^2 v}{\mathbf{R}}\)
The force is directed in the direction opposite to velocity of rod (u).

(b) Power, P = F × v = \(\frac{\mathbf{B}^2 l^2 v}{\mathbf{R}}\) × v = \(\frac{\mathbf{B}^2 l^2 v^2}{\mathbf{R}}\)
Hence, Power = \(\frac{\mathbf{B}^2 l^2 v^2}{\mathbf{R}}\)

Question 18.
Draw a ray diagram to show the image formation of a distant object by a refracting telescope. Write the expression for its angular magnification in terms of the focal lengths of the lenses used. State the important considerations required to achieve large resolution and their consequent limitations. [3]
Answer:
(i) Ray diagram of Astronomical telescope:

(ii) Angular Magnification, m = \(\frac{-f_0}{f_e}\)
(iii) For achieving large resolution, the objective of large aperture is required.
(iv) Consequent Limitations : It becomes very heavy and unmanageable, hence difficult to make and support by their edge and also suffers with chromatic aberrations.

Question 19.
An electromagnetic wave of wavelength λ is incident on a photosensitive surface of negligible work function. If the photoelectrons emitted from this surface have the de-Broglie wavelength λ ₁ , prove that λ = \(\left(\frac{2 m c}{h}\right) \lambda_1^2\). [3]
(a) An electron and a proton are accelerated through the same potential. Which one of the two has
(i) greater value of de-Broglie wavelength associated with it, and (ii) lesser momentum?
Justify your answer in each case.
(b) How is the momentum of a particle related with its de-Broglie wavelength? Show the variation on a graph.
Answer:
Photoelectric equation is hv = hv ₀ + E _K
As Work function is negligible
hv = E _K ….(i)
\(\frac{h c}{\lambda}\) = E _K …………(ii)
de-Broglie wavelength,
λ ₁ = \(\frac{h}{mv}\) = \(\frac{h}{\sqrt{2 m \mathrm{E}_{\mathrm{K}}}}\) ………….(iii)
Substituting the value of E _K from equation (ii) in equation (iii), we have

Or,

(a) Given: An electron and proton are accelerated through the same potential.

(b) λ = \(\frac{h}{p}\)

Question 20.
(a) Using Bohr’s postulates, derive the expression for the orbital period of the electron moving in the nth orbit of hydrogen atom.
(b) Write Rydberg’s formula for wavelengths of the spectral lines of hydrogen atom
spectrum. Mention to which series in the emission spectrum of hydrogen, H _α line belongs. [3]
Answer:
(a) The orbital period of electron in hydrogen atom is given by T = \(\frac{2 \pi r_n}{v_n}\)
From Bohr’s postulates, mv _n r _n = \(\frac{n h}{2 \pi}\)
We have r _n = \(\frac{n^2 h^2 \varepsilon_0}{\pi m e^2}\)
and velocity of electron in n ^th orbital, v _n = \(\frac{e^2}{2 \varepsilon_0 n h}\)
On substituting the values of rn and vn from equations (it) and (Hi) in equation (i) we have
T = 2π × \(\left(\frac{n^2 h^2 \varepsilon_0}{\pi m e^2}\right)\) ×{\(\frac{2 \varepsilon_0}{e^2} n h\)} = \(\frac{4 n^3 h^3 \varepsilon_0}{m e^4}\)

(b) (i) Rydberg’s formula for wavelengths of the spectral lines is: \(\frac{1}{\lambda}\) = R(\(\frac{1}{n_1^2}\) – \(\frac{1}{n_2^2}\))
(ii) H _α belongs to Balmer series.

Question 21.
Draw a graph showing the variation of binding energy per nucleon with mass number of different nuclei. Write any two salient features of the curve. How does this curve explain the release of energy both in the processes of nuclear fission and fusion? [3]
Answer:
(a) Binding Energy Curve:

Conclusions :
(i) The force is attractive and sufficiently strong to produce a binding energy of a few MeV per nucleon.
(ii) For mass number 2 to 20, there*are sharply defined peaks corresponding to ₂ Hg ⁴ , ₆ C ¹² , ₈ O ¹⁶ etc. The peak indicates that their nuclei are relatively mass stable than the other nuclei in their neighbourhood.

Question 22.
(a) Draw a ray diagram of compound microscope for the final image formed at least distance of distinct vision.
(b) An angular magnification of 30 is desired using an objective of focal length 1.25 cm and
an eye piece of focal length 5 cm. How will you set up the compound microscope for the final image formed at least distance of distinct vision. [3]
Answer:
(a) Diagram of Compound Microscope for the final image formed at distance D:

(b) Given. m ₀ = 30, f ₀ = 1.25 cm, f _e = 5 cm
When image is formed at least distance of distinct vision, D = 25 cm
Angular magnification of eyepiece, m _e = (1+\(\frac{D}{f_e}\)) = (1+\(\frac{25}{5}\)) = 1 + 5 = 6
Total Angular magnification, m = m ₀ m _e
⇒ m ₀ = \(\frac{m}{m_e}\) = \(\frac{30}{6}\) = 5
As the objective lens forms the real image,
m ₀ = \(-\frac{v_0}{u_0}\) = -5 ⇒ v ₀ = -5 u ₀

Thus, object is to be placed at 1.5 cm from the objective and separation between the two lenses should be
L = v ₀ + |u _e | = 75 + 4.17 = 11.67 cm

Question 23.
With what considerations in view is a photodiode fabricated? Explain its working with the help of a suitable diagram. With the help of V-I characteristics, state how photodiode is used to detect optical signals. [3]
Answer:
A photodiode is fabricated with a transparent window to allow light to fall on the diode. And the generation of e-h pairs takes place in or near the depletion region of the diode. For working of photodiode and for diagram ofV-l characteristic curves of photodiode :
Photo diodes. Photo diode is a special type of photo-detector. Simplest photo-diode is a reverse biased as shown in Figure (i).

When a p-n diode is illuminated with light photons having energy hv > E _g and intensities I ₁ , I ₂ , I ₃ etc. the electron and hole pairs generating in the depletion layer will be separated by the junction field and made to flow across the junction. Graph showing variation in reverse bias currents for different intensities are shown in Figure
(ii).