CBSE Class 12 Maths Question Paper 2019 (Series: BVM/1) with Solutions

Students can use CBSE Previous Year Question Papers Class 12 Maths with Solutions and CBSE Class 12 Maths Question Paper 2019 (Series: BVM/1) to familiarize themselves with the exam format and marking scheme.

CBSE Class 12 Maths Question Paper 2019 (Series: BVM/1) with Solutions

Time Allowed: 3 hours
Maximum Marks: 100

General Instructions:

1. All questions are compulsory,
2. This question paper contains 29 questions divided into four Sections A, B, C and D. Section A comprises of 4 questions of one mark each, Section B comprises of 8 questions of two marks each, Section C comprises of 11 questions of four marks each and Section D comprises of 6 questions of six marks each.
3. All questions in Section A are to be answered in one word, one sentence or as per the exact requirement of the question.
4. There is no overall choice. However, internal choice 1ms been provided in 1 question of Section A,
   2 questions of Section B and 2 questions of Section C. You have to attempt only one of the alternatives in all such questions.
5. Use of calculators is not permitted. You may ask for logarithmic tables, if required.

SET I Code No. 65/1/1
Section-A

Questions number 1 to 4 carry one mark each.

Question 1.
If A and B are square matrices of the same order 3, such that | A | = 2 and AB = 2I, write the value of | B |.
Solution:

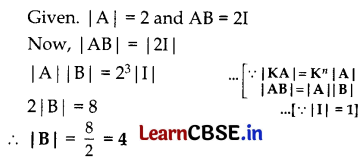
Question 2.
Write the number of all one-one functions from the set A = {a, b, c} to itself.
Solution:
A = {a, b, c}
The number of all one- from the set A are 3! = 6 one functions
(i) f(1) = 1, f(2) = 2, f(3) = 3
(ii) f(1) = 1 f(2) = 3, f(3) = 2
(iii) f(1) = 2, f(2) = 3, f(3) = 1
(iv) f(1) = 2, f(2) = 1, f(3) = 3
(v) f(1) = 3, f(2) = 2, f(3) = 1
(vi) f(1) = 3, f(2) = 1, f(3) = 2

Question 3.
Find the order and the degree of the differential equation x ² \(\frac{d^2 y}{d x^2}\) = \(\left\{1+\left(\frac{d y}{d x}\right)^2\right\}^4\)
Solution:
Order = 2
Degree = 1

Question 4.
If a line makes angles 90°, 135°, 45° with the x, y and z axes respectively, find its direction cosines.
Solution:
Here α = 90°, β = 135°, γ = 45°
We know, l = cos α = cos 90° = 0
m = cos β = cos 135° = cos(180° – 45°)
= – cos 45° = \(\frac{-1}{\sqrt{2}}\)
n = cos γ = cos 45° = \(\frac{1}{\sqrt{2}}\)
∴ Direction cosines are 0, \(-\frac{1}{\sqrt{2}}\), \(\frac{1}{\sqrt{2}}\).

Or

Yabby Casino has emerged as a popular choice for online gaming enthusiasts, offering a seamless experience from the moment you log in. The Yabby Casino login process is designed to be user-friendly, ensuring that players can easily access their accounts and dive into their favorite games within seconds.

To start, simply visit the official website and locate the login section. Input your credentials, and in no time, you’ll be ready to explore the wide array of slots, table games, and live dealer options available. As a player, keeping your account secure is crucial, and Yabby Casino prioritizes your safety by implementing advanced encryption protocols. If you face any issues during the login process, their customer support team is always ready to assist you.

For more detailed information and support regarding the login process, you can click on this link: https://yabbycasinologin.net/ . Enjoy a world of gaming entertainment with just a few clicks!

Find the vector equation of the line which passes through the point (3, 4, 5) and is parallel to the vector 2\(\hat{i}\) + 2\(\hat{j}\) – 3\(\hat{k}\).
Solution:

Section – B

Questions number 5 to 12 carry 2 marks each.

Question 5.
Check whether the relation R in the set R of real number, defined by R = {(a, b): 1 + ab > 0}, is reflexive, symmetric or transitive. ”
Solution:

Question 6.
Find a matrix A such that 2A – 3B + 5C = 0, where B = \(\left[\begin{array}{rrr}
-2 & 2 & 0 \\
3 & 1 & 4
\end{array}\right]\) and C = \(\left[\begin{array}{rrr}
2 & 0 & -2 \\
7 & 1 & 6
\end{array}\right]\)
Solution:
2A – 3B + 5C = 0
⇒ 2A = 3B – 5C

Question 7.
Find: \(\int \frac{\sec ^2 x}{\sqrt{\tan ^2 x+4}} d x\)
Solution:

Question 8.
Find: \(\int \sqrt{1-\sin 2 x}\) dx, \(\frac{\pi}{4}\) < x < \(\frac{\pi}{2}\)
Solution:

Or

Find: ∫sin ^-1 (2x)dx.
Solution:
Let I = ∫sin ^-1 (2x).1 dx
Integration by parts taking ‘1’ as second function,

Question 9.
Find the particular solution of the differential equation:
(1 + e ^2x ) dy + (1 + y ² ) ex dx = 0, given that y = 1, when x = 0.
Solution:

Question 10.
If the sum of two unit vectors is a unit vector, prove that the magnitude of their difference is \(\sqrt{3}\).
Solution:

Question 11.
A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be the event “number is even” and B be the event “number is marked red”. Find whether the events A and B are independent or not.
Solution:
Number obtained is even, i.e., A = 2, 4, 6
Number obtained is red, i.e.. B = 1, 2, 3
∴ P(A) = \(\frac{3}{6}\) = \(\frac{1}{2}\), P(B) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
P(A ∩ B) = P(even red number)
= P(number 2) = \(\frac{1}{6}\)
P(A) × P(B) = \(\frac{1}{2} \times \frac{1}{2}\) = \(\frac{1}{4}\)
⇒ P(A) × P(B) ≠ P(A ∩ B)
Hence, A and B are not independent events.

Question 12.
A bag contains 4 red and 4 black balls, another bag contains 2 red and 6 black balls. One of the two bags is selected at random and two balls are drawn at random (without replacement) from the bag which are both found to be red. Find the probability that the balls are drawn from the first bag.
Solution:
Let E ₁ be the event that the first bag is selected.
Let E ₂ be the event that the second bag is selected
Let A be the event that both balls are red.

Or

The random variable X has a probability distribution P(X) of the following form, where ‘k’ is some number.

Determine the value of ‘k’.
Solution:
P(0) + P(1) + P(2) = 1
⇒ k + 2k + 3k = 1
⇒ 6k = 1
∴ k = \(\frac{1}{6}\)

Section-C

Questions number 13 to 23 carry 4 marks each.

Question 13.
Show that the relation R on R defined as R = {(a, b): a ≤ b], is reflexive, and transitive but not symmetric.
Solution:
R = {(a, b) : a ≤ b)
Clearly (a, a) ∈ R as a ≤ a is true
∴ R is reflexive.
Now (2, 4) ∈ R (as 2 < 4)
But (4, 2) ∉ R as 4 is greater than 2
∴ R is not symmetric
Now Let (a, b), (b, c) ∈ R
Then a ≤ b, b ≤ c
⇒ a ≤ c ⇒ (a, c) ∈ R
∴ R is a transitive
Hence, R is reflexive and transitive but not symmetric.

Question 14.
Solve: tan ^-1 4x + tan ^-1 6x = \(\frac{\pi}{4}\).
Solution:

Since x = \(\frac{-1}{2}\) does not satisfy the equation, as the LH.S of the equation becomes negative.
∴ x = \(\frac{1}{12}\) is the only solution of the given equation.

Question 15.
If A = \(\left[\begin{array}{ccc}
2 & 3 & 4 \\
1 & -1 & 0 \\
0 & 1 & 2
\end{array}\right]\), find A ^-1 . Hence, solve the system of equations.
x – y = 3;
2x + 3y + 4z = 17;
y + 2z = 7
Solution:

Question 16.
If log (x ² + y ² ) = 2 tan ^-1 \(\left(\frac{y}{x}\right)\), show that \(\frac{d y}{d x}\) = \(\frac{x+y}{x-y}\).
Solution:

Or

If x ^y – y ^x = a ^b , find \(\frac{d y}{d x}\).
Solution:
Let A = x ^y
Taking log on both sides, we have
log A = log x ^y
log A = y log x [∵ logm ⁿ = nlogm]
Differentiating both sides w.r.t. x, we have
\(\frac{1}{\mathrm{~A}} \frac{d \mathrm{~A}}{d x}\) = y.\(\frac{1}{x}\) + log x.\(\frac{d y}{d x}\)

Question 17.
If y = (sin ^-1 x) ² , prove that (1 – x ² )\(\frac{d^2 y}{d x^2}\) – x\(\frac{d y}{d x}\) – 2 = 0.
Solution:

Question 18.
Find the intervals in which the function f(x) = (x – 1) (x – 2) ² is (a) increasing, (b) decreasing.
Solution:
f(x) = (x – 1) (x – 2) ²
Differentiating both sides, w.r.t. x, we get
f’(x) = (x – 1).2(x – 2) + (x- 2) ² .1
= (x – 2)[2x – 2 + x – 2]
= (x – 2) (3x – 4)
For stationary point,f’(x) = 0
∴ (3x – 4) = 0 or (x – 2) = 0
⇒ 3x = 4 or x = 2
⇒ x = \(\frac{4}{3}\) or x = 2

Question 19.
Find: \(\int \frac{3 x+5}{x^2+3 x-18} d x\)
Solution:

Question 20.
Prove that \(\int_0^a f(x) d x\) = \(\int_0^a f(a-x) d x\), hence evaluate \(\int_0^\pi \frac{x \sin x}{1+\cos ^2 x} d x\).
Solution:

Question 21.
Solve the differential equation: x dy – y dx = \(\sqrt{x^2+y^2}\) dx, given that y = 0 when x = 1.
Solution:

Or

Solve the differential equation: (1 + x ² )\(\frac{d y}{d x}\) + 2xy – 4x ² = 0, subject to the initial condition y(0) = 0.
Solution:

Question 22.
If \(\hat{i}\) + \(\hat{j}\) + \(\hat{k}\), 2\(\hat{i}\) + 5 \(\hat{j}\), 3\(\hat{i}\) + 2\(\hat{j}\) – 3\(\hat{k}\) and \(\hat{i}\) – 6\(\hat{j}\) – \(\hat{k}\) respectively are the position vectors of points A, B, C and D, then find the angle between the straight lines AB and CD. Find whether AB and CD are collinear or not.
Solution:

Question 23.
Find the value of λ, so that the lines \(\frac{1-x}{3}\) = \(\frac{7 y-14}{\lambda}\) = \(\frac{z-3}{2}\) and \(\frac{7-7 x}{3 \lambda}\) = \(\frac{y-5}{1}\) = \(\frac{6-z}{5}\) are at right angles. Also, find whether the lines are intersecting or not.
Solution:


Putting the value of p & q in (vi),
\(\frac{3}{7}\) + 2 = \(\frac{3}{7}\) + 5 ⇒ \(\frac{17}{7}\) ≠ \(\frac{38}{7}\), which is not true.
∴ Given lines are not intersecting each other.

Section – D

Questions number 24 to 29 carry 6 marks each.

Question 24.
If A = \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 0 & 2 \\
3 & 1 & 1
\end{array}\right]\), find A ^-1 . Hence, solve the system of equations
x + y + 2 = 6, x + 2z = 7, 3x + y + z = 12.
Solution:
Given equations can be written as

Question 25.
A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m ³ . If building of tank costs ₹70 per square metre for the base and ₹45 per square metre for the sides, what is the cost of least expensive tank?
Solution:
Let x m be the length and y m be the breadth of open tank.

Volume of tank (lbh) = 8m ³ ……[Given
⇒ xy(2) = 8 ………[∵ h = 2m
⇒ y = \(\frac{4}{x}\) ……. (i)
Surface area of open tank
= Area of base + Area of 4 waIls
= lb + 2h(l + b) = xy + 2(2)(x + y) = xy + 4(x + y)
According to the Question,
Total Cost, C = 70(xy) + 45[4(x + y)]
C = 70x\(\left(\frac{4}{x}\right)\) + 180(x + \(\frac{4}{x}\)) ….. [from (i)]

∴ Total cost is minimum at x = 2m
Putting the value of x in (ii)
Minimum total cost,
∴ C = 280 + 180(2) + \(\frac{720}{2}\)
= 280 + 360 + 360 = ₹ 1,000
Therefore, the cost of expensive tank is ₹1000.

Question 26.
Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
Solution:
Let A(2, 5), B(4, 7) and C(6, 2)

⇒ x(5 – 7) – y(2 – 4) + 1(14 – 20) = 0
⇒ -2x + 2y – 6 = 0
⇒ 2y = 2x + 6 ⇒ y = x + 3

∴ Shaded Area = Area of region ABEDA + Area of region BCFEB – Area of region ACFDA

Question 27.
If lines \(\frac{x-1}{2}\) = \(\frac{y+1}{3}\) = \(\frac{z-1}{4}\) and \(\frac{x-3}{1}\) = \(\frac{y-k}{2}\) = \(\frac{z}{1}\) intersect, then find the value of k.
Solution:

Expanding along R ₁ , we have
2(3 – 8) – (k + 1)(2 – 4) – 1(4 – 3) = 0
-10 + 2k + 2 – 1 = 0
2k = 9 ⇒ k = \(\frac{9}{2}\)

Question 28.
A manufacturer has three machine operators A, B and C. The first operator A produces 1%
of defective items, whereas the other two operators B and C produce 5% and 7% defective items respectively. A is on the job for 50% of the time, B on the job 30% of the time and C on the job for 20% of the time. All the items are put into one stockpile and then one item is chosen at random from this and is found to be defective. What is the probability that it was produced by A?
Solution:
Let Event E ₁ : items produced by A
E ₂ : items produced by B
E ₃ : items produced by C
Let the event B be the defective items.

Question 29.
A manufacturer has employed 5 skilled men and 10 semi-skilled men and makes two models A and B of an article. The making of one item of model A requires 2 hours work by a skilled man and 2 hours work by a semi-skilled man. One item of model B requires 1 hour by a skilled man and 3 hours by a semi-skilled man. No man is expected to work more than 8 hours per day. The manufacturer’s profit on an item of model A is ₹15 and on an item of model B is ₹10. How many of items of each model should be made per day in order to maximize daily profit? Formulate the above LPP and solve it graphically and find the maximum profit.
Solution:

Let x and y be the number of items of models A and B respectively.
Maximum Profit, Z = ₹(15x + 10y)
Subject to the constraints:
2 + 1y ≤ 40
2x + 3y ≤ 80, x ≥ 0, y ≥ 0


Hence Maximum value of z is ₹350 attained at the point C(10, 20).
Hence, 10 items of Model A and 20 items of Model B gives the maximum profit of ₹350.

SET II Code No. 65/1/2

Note: Except for the following questions, all the remaining questions have been asked in Set-I.

Question 3.
Find the value of x – y, if
2\(\left[\begin{array}{ll}
1 & 3 \\
0 & x
\end{array}\right]\) + \(\left[\begin{array}{ll}
y & 0 \\
1 & 2
\end{array}\right]\) = \(\left[\begin{array}{ll}
5 & 6 \\
1 & 8
\end{array}\right]\)
Solution:

Question 6.
If A = \(\left[\begin{array}{ccc}
2 & 0 & 1 \\
2 & 1 & 3 \\
1 & -1 & 0
\end{array}\right]\), then find (A ² – 5A).
Solution:

Question 12.
Find: \(\int \frac{\tan ^2 x \sec ^2 x}{1-\tan ^6 x} d x\)
Solution:

Question 19.
If x = cos t + log tan \(\left(\frac{t}{2}\right)\), y = sin t, then find the value of \(\frac{d^2 y}{d t^2}\) and \(\frac{d^2 y}{d x^2}\) at t = \(\frac{\pi}{4}\).
Solution:

Question 24.
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is \(\frac{4 r}{3}\). Also find the maximum volume of cone.
Solution:

Question 25.
If A = \(\left[\begin{array}{ccc}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\), then find A ^-1 . Hence solve the following system of equations:
2x – 3y + 5z = 11; 3x + 2y – 4z = -5; x + y – 2z = -3.
Solution:
Given equations can be written as
AX = B ⇒ X = A ^-1 B ……… (i)

SET III Code No. 65/1/3

Note: Except for the following questions, all the remaining questions have been asked in Set-I and Set-II.

Question 1.
If 3A – B = \(\left[\begin{array}{ll}
5 & 0 \\
1 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{ll}
4 & 3 \\
2 & 5
\end{array}\right]\), then find the matrix A.
Solution:

Question 2.
Write the order and the degree of the following equation:
\(x^3\left(\frac{d^2 y}{d x^2}\right)^2\) + x\(x\left(\frac{d y}{d x}\right)^4\) = 0
Solution:
Order = 2, Degree = 2

Question 5.
Find : ∫sinx.log cos x dx
Solution:

Question 6.
Evaluate: ∫ (1 – x ² )sinxcos ² xdx
Solution:

Or

Evaluate: \(\int_{-1}^2 \frac{|x|}{x} d x\).
Solution:

Question 20.
Find: \(\int \frac{\cos x}{(1+\sin x)(2+\sin x)} d x\).
Solution:

Question 21.
Solve the differential equation: \(\frac{d y}{d x}-\frac{2 x}{1+x^2}\) = x ² + 2.
Solution:

Or

Solve the differential equation: (x + 1)\(\frac{d y}{d x}\) = 2e ^-y – 1; y(0) = 0.
Solution:

Question 26.
Using integration, find the area of the triangle whose vertices are (2, 3), (3, 5) and (4, 4).
Solution:

⇒ -2x + y + 1 = 0 ⇒ y = (2x – 1) …….. (i)

Question 29.
Two cards are drawn simultaneously (or successively without replacement) from a well shuffled pack of 52 cards. Find the mean of the number of kings.
Solution:
Total number of cards = 52
Number of kings =4
∴ Total number of remaining cards = 48
Let X be the event that king card is drawn.
∴ X can take values 0, 1, 2.
P(X = 0) = P(No. king cards)
= \(\frac{{ }^{48} C_2}{{ }^{52} C_2}\) = \(\begin{aligned}
& 48 \times 47 \\
& \frac{2 \times 1}{\frac{52 \times 51}{2 \times 1}} \\
&
\end{aligned}\) = \(\frac{188}{221}\)