Students can use CBSE Previous Year Question Papers Class 12 Maths with Solutions and CBSE Class 12 Maths Question Paper 2018 Comptt (Delhi & Outside Delhi) to familiarize themselves with the exam format and marking scheme.
CBSE Class 12 Maths Question Paper 2018 Comptt (Delhi & Outside Delhi) with Solutions
Time Allowed: 3 hours
Maximum Marks: 100
General Instructions:
- All questions are compulsory.
- The Question Paper consists of 29 questions divided into four Sections A, B, C and D. Section-A comprises of 4 questions of one mark each, Section-B comprises of 8 questions of two marks each, Section-C comprises of 11 questions of four marks each and Section-D comprises of 6 questions of six marks each.
- All questions in Section-A are to be answered in one word, one sentence or as per the exact requirement of the question.
- There is no overall choice. However, internal choice has been provided in 3 questions of four marks each and 3 questions of six marks each.
- Use of calculators is not permitted. You may ask for logarithmic tables, if required.
-
HashLucky Casino is quickly making a name for itself in the Australian online gaming scene. With a user-friendly interface and a diverse range of games, it caters to both novice and seasoned players. The casino offers a wide array of slot machines, table games, and live dealer experiences, ensuring that there’s something for everyone.
One of the standout features of HashLucky Casino is its commitment to player security and fairness. Utilizing advanced encryption technologies, it protects players’ data and transactions, allowing for a safe gaming environment. Additionally, the casino offers generous bonuses and promotions, enhancing the overall gaming experience.
Players can easily access the casino through its website https://hashluckylogin.casino/ , where they can find detailed information on promotions, game rules, and customer support options. With a responsive customer service team available around the clock, players can enjoy peace of mind while having fun.
Overall, HashLucky Casino offers an exciting and secure online gambling experience for Australian players, making it a top choice in the competitive market.
Section-A
Questions number 1 to 4 carry one mark each.
Question 1.
Find the value of tan
-1
\(\sqrt{3}\) – sec
-1
(-2).
Solution:
Given tan
-1
\((\sqrt{3})\) – sec
-1
(-2)
= \(\frac{\pi}{3}\) – [π – sec
-1
(2)]
….[∵ sec
-1
(-x) = π – sec-1x, |x| ≥ 1]
= \(\frac{\pi}{3}\) – π + \(\frac{\pi}{3}\) = –\(\frac{\pi}{3}\)
Question 2.
If A = \(\left(\begin{array}{rrr}
1 & 2 & 2 \\
2 & 1 & x \\
-2 & 2 & -1
\end{array}\right)\) is a matrix satisfying AA’ = 9I, find x.
Solution:

Question 3.
Two cards are drawn at random from a pack of 52 cards one-by-one without replacement. What is the probability of getting first card red and second card Jack?
Solution:
The Required Probability = P(The first is a red jack and the second is a jack card) or (The first is a red non-jack card and the second is a jack card)
= \(\frac{2}{52} \times \frac{3}{51}\) + \(\frac{24}{52} \times \frac{4}{51}\) = \(\frac{1}{26}\)
![]()
Question 4.
The position vectors of point A and B are \(\vec{a}\) and \(\vec{b}\) respectively.
P divides AB in the ratio 3 : 1 and Q is mid-point of AP. Find the position vector of Q.
Solution:
Coordinates of point P
= \(\frac{3(\vec{a})+1(\vec{b})}{3+1}\) = \(\frac{3 \vec{a}+\vec{b}}{4}\)
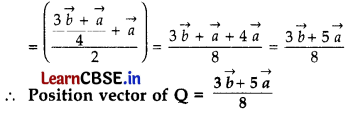
Section – B
Questions number 5 to 12 carry 2 marks each.
Question 5.
Prove that: 3 cos
-1
x = cos
-1
(4x
3
– 3x), x ∈ [\(\frac{1}{2}\), 1].
Solution:
RH.S. = cos
-1
(4x
3
– 3x)
= cos
-1
(4 cos
3
θ – 3 cos θ) [Let x = cosθ ∴ cos
-1
x = θ]
= cos
-1
(cos3θ) = 3θ
= 3 cos
-1
x = L.H.S. (Hence proved)
Question 6.
If A = \(\left[\begin{array}{rr}
2 & 3 \\
5 & -2
\end{array}\right]\) be such that A
-1
= kA, then find the value of k.
Solution:

⇒ 2k = \(\frac{2}{19}\)
………… [Equating the corresponding elements
∴ k = \(\frac{1}{19}\)
Question 7.
Differentiate tan
-1
\(\left[\frac{\cos x-\sin x}{\cos x+\sin x}\right]\) with respect to x.
Solution:
Let y = tan
-1
\(\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)\)
Dividing Numerator and Denominator by cos x, we have
y = tan
-1
\(\left(\frac{1-\tan x}{1+\tan x}\right)\)
y = tan
-1
\(\left(\tan \left(\frac{\pi}{4}-x\right)\right)\)
y = \(\frac{\pi}{4}\) – x
Differentiating both sides w.r.t. x, we have \(\frac{d y}{d x}\) = -1
\(\frac{d y}{d x}\) = -1
Question 8.
The total revenue received from the sale of x units of a product is given by R(x) = 3x
2
+ 36x + in rupees. Find the marginal revenue when x = 5, where by marginal revenue we mean the rate of change of total revenue with respect to the number of items sold at an instant.
Solution:
R(x) = 3x
2
+ 36x + 5
Differentiating both sides w.r.t. x, we have
Marginal Revenue, R'(x) = 6x + 36
When x = 5, R'(5) = 6(5) + 36
= 30 + 36 = ₹ 66
∴ Marginal Revenue is ₹ 66.
Question 9.
Find: \(\int \frac{3-5 \sin x}{\cos ^2 x}\)dx
Solution:

Question 10.
Solve the differential equation cos\(\left(\frac{d y}{d x}\right)\) = a, (a ∈ IR).
Solution:
cos \(\left(\frac{d y}{d x}\right)\) = a
\(\frac{d y}{d x}\) = cos
-1
a
dy = cos
-1
a∫dy ……… [Integrating both sides]
y = x . cos
-1
a + C
y – C = x cos
-1
a
\(\frac{y-C}{x}\) = cos
-1
a
cos\(\left(\frac{y-C}{x}\right)\) = a is the solution of the differential equation.
![]()
Question 11.
If \(\vec{a}+\vec{b}+\vec{c}\) = \(\overrightarrow{0}\) and \(|\vec{a}|\) = 5, \(|\vec{b}|\) = 6 and \(|\vec{c}|\) = 9, then find the angle between a and b.
Solution:

Question 12.
Evaluate: P(A ∪ B), if 2P(A) = P(B) = \(\frac{5}{13}\) and P(A | B) = \(\frac{2}{5}\).
Solution:

Section-C
Questions number 13 to 23 carry 4 marks each.
Question 13.
Evaluate: \(\int_{-1}^2\left|x^3-3 x^2+2 x\right|\) dx
Solution:
The given definite integral
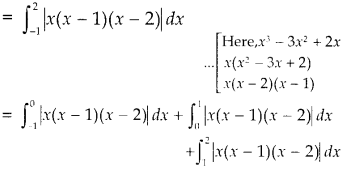

Question 14.
If sin y = x cos(a + y), then show that \(\frac{d y}{d x}\) = \(\frac{\cos ^2(a+y)}{\cos a}\)
Also, show that \(\frac{d y}{d x}\) = cos a, when x = 0.
Solution:

Question 15.
If x = a sec
3
θ and y = a tan
3
θ, find \(\frac{d^2 y}{d x^2}\) at θ = \(\frac{\pi}{3}\).
Answer:

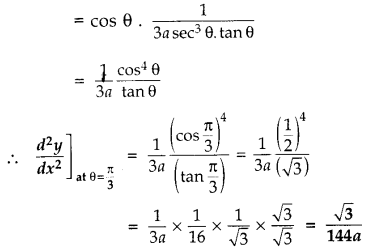
Or
If y = \(e^{\tan ^{-1} x}\), prove that (1 + x
2
)\( + (2x – 1)[latex]\frac{d y}{d x}\) = 0.
Solution:

Question 16.
Find the intervals in which the function f(x) = -2x
3
– 9x
2
– 12x + 1 is
(i) Strictly increasing,
(ii) Strictly decreasing.
Solution:
f(x) = -2x
3
– 9x
2
– 12x + 1
Differentiating both sides w.r.t. x, we have
f’(x) = -6x
2
– 18x – 12
= -6(x
2
+ 3x + 2)
= -6(x
2
+ 2t + x + 2)
= -6[x(x + 2) + 1(x + 2)]
= -6(x + 2) (x + 1)
When f’(x) = 0, x = -2, -1

(i) f is strictly increasing in (-2, -1).
(ii) f is strictly decreasing in (-∞, -2) ∪ (-1, ∞).
Question 17.
A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 metres. Find the dimensions of the window to admit maximum light through the whole opening.
Solution:
Let length of rectangular window = 2x m
Let breadth of rectangular window = y m
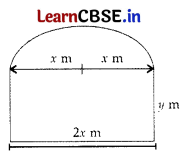
∴ Radius of rectangular window = x m
Perimeter of window = 10 m
∴ y + 2x + y + πx = 10
…..[∵ Perimeter of semi-circle = πr
2y = 10 – 2x – πx
y = \(\frac{10-2 x-\pi x}{2}\) ……….. (i)
y = \(\left(5-x-\frac{\pi}{2} x\right)\)
Area of window = Area of rectangle + Area of semi-circle

∴ Area is maximum at x = \(\frac{10}{4+\pi}\) m
∴ Maximum light will enter the window when radius = \(\frac{10}{4+\pi}\) m.
Length of rectangle window
= 2x = \(\frac{20}{4+\pi}\) m,
Breadth of rectangle window, y
= 5 – \(\frac{10}{4+\pi}\) – \(\frac{\pi}{2}\left(\frac{10}{4+\pi}\right)\)
= \(\frac{20+5 \pi-10-5 \pi}{4+\pi}\) = \(\frac{10}{4+\pi}\) m
![]()
Question 18.
Find: \(\int \frac{4}{(x-2)\left(x^2+4\right)}\) dx.
Solution:

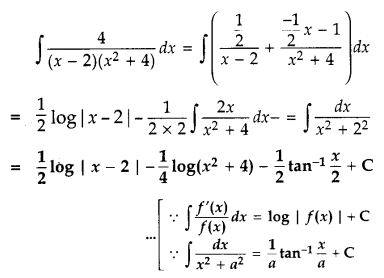
Question 19.
Solve the differential equation (x
2
– y
2
) dx + 2xy dy = 0.
Solution:

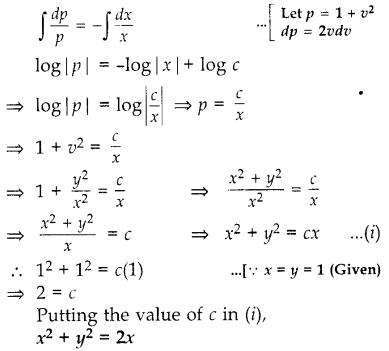
Or
Find the particular solution of the differential equation (1 + x
2
)\(\frac{d y}{d x}\) + 2xy = \(\frac{1}{1+x^2}\), given that y = 0 when x = 1.
Solution:

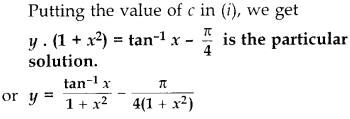
Question 20.
Find the value of λ so that the lines \(\frac{1-x}{3}\) = \(\frac{7 y-14}{2 \lambda}\) = \(\frac{5 z-10}{11}\) and \(\frac{7-7 x}{3 \lambda}\) = \(\frac{y-5}{1}\) = \(\frac{6-z}{5}\) are perpendicular to each other.
Solution:

Question 21.
Find the shortest distance between the lines \(\frac{x-1}{2}\) = \(\frac{y-2}{3}\) = \(\frac{z-3}{4}\) and \([\frac{x-2}{3}/latex] = [latex]\frac{y-4}{4}\) = \(\frac{z-5}{5}\).
Answer:

Question 22.
Two groups are competing for the positions of the Board of Directors of a corporation. The probabilities that the first and second group will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3 if the second group wins. Find the probability that the new product introduced was by the second group.
Solution:
Let E
1
, E
2
, A be the following events.
E
1
: 1
st
group will win
E
2
: 2
nd
group will win
A : Introducing a new product
P(E
1
) = 0.6, P(A | E
1
) = 0.7
P(E
2
) = 0.4, P(A | E
2
) = 0.3
Using Bayes’ theorem,

Question 23.
From a lot of 20 bulbs which include 5 defectives, a sample of 3 bulbs is drawn by random, one by one with replacement. Find the probability distribution of the number of defective bulbs. Also, find the mean of the distribution.
Solution:

Section-D
Questions number 24 to 29 carry 6 marks each.
Question 24.
Show that the relation R on the set Z of all integers defined by (x, y) ∈ R ⇔ (x – y) is divisible by 3 is an equivalence relation.
Solution:
R = {(x, y): x, y ∈ Z and (x – y) is divisible by 3}
Reflexive: R is reflexive, for x ∈ Z
x – x = 0, which is divisible by 3
(x, x) ∈ R ∴ R is reflexive.
Symmetric:
R is symmetric, (x, y) ∈ R where x, y ∈ Z
x – y is divisible by 3.
Let (x – y) = 3 m, where in m ∈ Z
-(y – x) = 3 m
(y – x) = -3 m
(y – x) is divisible by 3.
(y – x) ∈ R ∴ R is symmetric.
Transitive:
R is transitive, (x, y) ∈ R where x, y ∈ Z
x – y is divisible by 3.
x – y = 3 in, where m ∈ Z
For (y, z) ∈ Z, where y, Z ∈ Z
y – z is divisible by 3.
y – z = 3 n, where n ∈ Z …….(ii)
Adding (i) and (ii),
(x – y) + (y – z) = 3m + 3n
x – z = 3(m+n)
⇒ (x – z) is divisible by 3.
(x, y) ∈ R, (y, z) ∈ R
∴ (x, z) ∈ R where x, y, z ∈ Z
R is transitive.
Since R is reflexive, symmetric and transitive.
∴ R is an equivalence relation.
![]()
Question 25.
Given A = \(\left[\begin{array}{lll}
5 & 0 & 4 \\
2 & 3 & 2 \\
1 & 2 & 1
\end{array}\right]\), B
-1
= \(\left[\begin{array}{lll}
1 & 3 & 3 \\
1 & 4 & 3 \\
1 & 3 & 4
\end{array}\right]\), compute (AB)
-1
.
Solution:

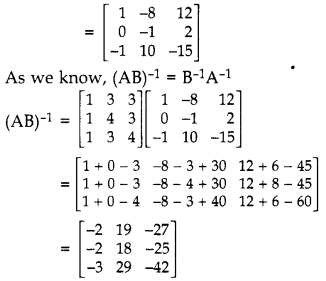
Question 26.
Using integration, find the area of the region: {(x, y) : 0 ≤ 2y ≤ x
2
, 0 ≤ y ≤ x, 0 ≤ x ≤ 3}
Solution:

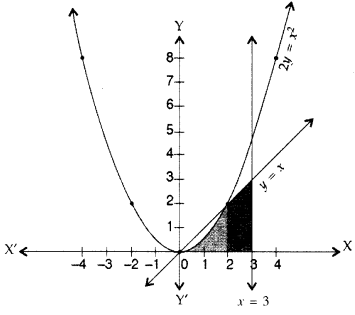
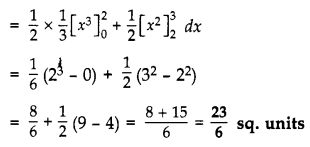
Question 27.
Evaluate: \(\int_0^{\pi / 2} \frac{x \sin x \cos x}{\sin ^4 x+\cos ^4 x}\) dx.
Solution:


Question 28.
Find the angle between the following pair of lines : \(\frac{-x+2}{-2}\) = \(\frac{y-1}{7}\) = \(\frac{z+3}{-3}\) and \(\frac{x+2}{-1}\) = \(\frac{2 y-8}{4}\) = \(\frac{z-5}{4}\) and check whether the lines are parallel or perpendicular.
Solution:

Question 29.
A company produces two types of goods, A and B, that require gold and silver. Each unit of type A requires 3 g of silver and 1 g of gold while that of B requires 1 g of silver and 2 g of gold. The company can use at most 9 g of silver and 8 g of gold. If each unit of type A brings a profit of ₹40 and that of type B ₹50, find the number of units of each type that the company should produce to maximize the profit. Formulate and solve graphically the LPP and find the maximum profit.
Solution:
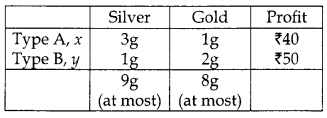
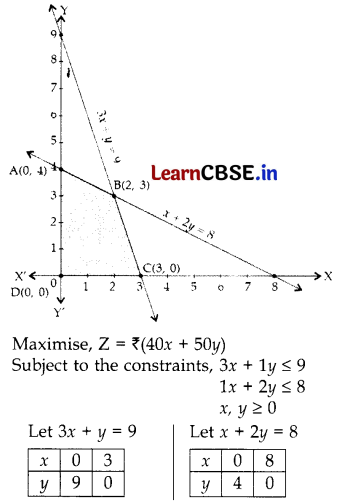
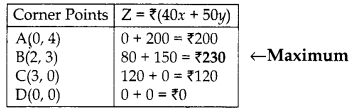
Maximum value of Z is ₹ 230 at B(2, 3) i.e., the company should produce 2 units of Type A and 3 units of Type B goods to maximize the Profit.