CBSE Class 10 Maths Question Paper 2023 (Series: WX1YZ/6) with Solutions

Students can use CBSE Previous Year Question Papers Class 10 Maths with Solutions and CBSE Class 10 Maths Question Paper 2023 (Series: WX1YZ/6) to familiarize themselves with the exam format and marking scheme.

CBSE Class 10 Maths Question Paper 2023 (Series: WX1YZ/6) with Solutions

Time allowed: 3 hours
Maximum marks: 80

General Instructions:
Read the following instructions carefully and follow them:

1. This question paper contains 38 questions. All questions are compulsory.
2. Question paper is divided into FIVE Sections – Section A, B, C, D and E.
3. In Section A – Question no. 1 to 18 are Multiple Choice Questions (MCQ) and Question number 19 and 20 are Assertion-Reason based questions of 1 mark each.
4. In Section B – Question number 21 to 25 are Very Short Answer (VSA) type questions of 2 marks each.
5. In Section C – Question number 26 to 31 are Short Answer (SA) type questions, carrying 3 marks each.
6. In Section D – Question number 32 to 35 are Long Answer (LA) type questions carrying 5 marks each.
7. In Section E – Question number 36 to 38 are case study based integrated units of assessment questions
   carrying 4 marks each. Internal choice is provided in 2 mark questions in each Case-study.
8. There is no overall choice. However, an internal choice has been provided in 2 questions in Section B, 2 questions in Section C, 2 questions in Section D and 3 questions in Section E.
9. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.
10. Use of calculators is NOT allowed.

SET I Code No. 30/6/1
Section – A (Multiple choice questions)

Section A consists of 20 questions of 1 mark each.
Question 1.
If P ² = \(\frac{32}{50}\), then P is a/an
(a) whole number
(b) integer
(c) rational number
(d) irrational number
Answer:
(c) rational number
We have, p ² = \(\frac{32}{50}\) = \(\frac{16}{25}\)
∴ p = ± \(\frac{4}{5}\) (Rational Number)

Question 2.
The distance of the point (-6, 8) from x-axis is
(a) 6 units
(b) -6 units
(c) 8 units
(d) 10 units
Answer:
(c) 8 units
8 units (ordinate)

Question 3.
The number of quadratic polynomials having zeroes -5 and -3 is 1
(a) 1
(b) 2
(c) 3
(d) more than 3
Answer:
(d) more than 3
Sum of zeroes, S = -5 + (-3) = -8
Product of zeroes, P = (-5) x (-3) = 15
∴ Quadratic Polynomial = k (x ² – Sx + P)
= k(x ² + 8x +15) …[Where k is non-zero real number
∴ Infinitely many Quadratic Polynomials are possible.

Question 4.
The point of intersection of the line represented by 3x – y = 3 and y-axis is given by 1
(a) (0,-3)
(b) (0, 3)
(c) (2, 0)
(d) (-2, 0)
Answer:
(a) (0,-3)
(a) Given. 3x – y = 3
⇒ 0 – y = 3 (At Y-axis Put x = 0)
∴ y = -3 ∴ Point = (x, y) = (0, -3)

Question 5.
The circumferences of two circles are in the ratio 4 : 5. What is the ratio of their radii? 1
(a) 16 : 25
(b) 25 : 16
(c) 2 : √5
(d) 4 : 5
Answer:
(d) 4 : 5
Let c ₁ and c ₂ be the circumferences of two circles respectively.
Given. \(\frac{c_1}{c_2}\) = \(\frac{1}{2}\) ⇒ \(\frac{2 \pi r_1}{2 \pi r_2}\) = \(\frac{1}{2}\)
∴ r ₁ : r ₂ = 4 : 5

Question 6.
If α and β are the zeroes of the polynomial x ² – 1, then the value of (α + β) is 1
(a) 2
(b) 1
(c) -1
(d) 0
Answer:
(d) 0
Given, x ² – 1 = 0
Here, a = 1, b = 0, c = -1
∴ α + β = \(\frac{-b}{a}=\frac{- \text { coefficient of } x}{\text { coefficient of } x^2}\)
= \(\frac{-0}{1}\) = 0

Question 7.
\(\frac{\cos ^2 \theta}{\sin ^2 \theta}-\frac{1}{\sin ^2 \theta}\), in simplified form, is: 1
(a) tan ² θ
(b) sec ² θ
(c) 1
(d) -1
Answer:
(d) -1
1 ^st Method: \(\frac{\cos ^2 \theta}{\sin ^2 \theta}-\frac{1}{\sin ^2 \theta}\)
= \(\frac{\cos ^2 \theta-1}{\sin ^2 \theta}\) = \(\frac{-\left(1-\cos ^2 \theta\right)}{\sin ^2 \theta}\) = \(\frac{-\sin ^2 \theta}{\sin ^2 \theta}\) = -1

2 ^nd Method: \(\frac{\cos ^2 \theta}{\sin ^2 \theta}-\frac{1}{\sin ^2 \theta}\)
= cot ² θ – cosec ² θ
= -(cosec ² θ – cot ² θ) = -1

Question 8.
If ΔPQR ~ ΔABC; PQ = 6 cm , AB = 8 cm and the perimeter of ΔABC is 36 cm, then the perimeter of ΔPQR is 1
(a) 20.25 cm
(b) 27 cm
(c) 48 cm
(d) 64 cm
Answer:
(b) 27 cm
ΔPQR ~ ΔABC

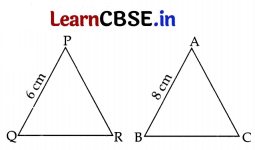
∴ Peri. (ΔPQR) = \(\frac{1}{2}\) × 36 = 27 cm

Question 9.
If the quadratic equation ax ² + bx + c = 0 has two real and equal roots, then ‘c’ is equal to’
(a) \(\frac{-b}{2 a}\)
(b) \(\frac{b}{2 a}\)
(c) \(\frac{-b^2}{4 a}\)
(d) \(\frac{b^2}{4 a}\)
Answer:
(d) \(\frac{b^2}{4 a}\)
D = 0 …[Since Roots are real and equal
⇒ b ² – 4ac = 0 ⇒ b ² = 4ac ∴ c = \(\frac{b^2}{4 a}\)

Question 10.
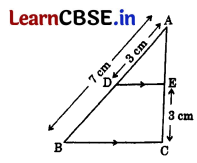
In the given figure, DE || BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then the length of AE is 1

(a) 2 cm
(b) 2.25 cm
(c) 3.5 cm
(d) 4 cm
Answer:
(b) 2.25 cm

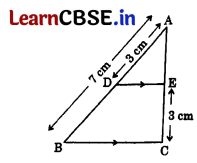
In ΔABC, DE || BC …[Given
\(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\) …[Thales theorem
⇒ \(\frac{3}{7-3}=\frac{\mathrm{AE}}{3}\) ⇒ 4 AE = 9
∴ AE = \(\frac{9}{4}\) = 2.25 cm

Question 11.
A bag contains 5 pink, 8 blue and 7 yellow balls. One ball is drawn at random from the bag. What is the probability of getting neither a blue nor a pink ball? 1
(a) \(\frac{1}{4}\)
(b) \(\frac{2}{5}\)
(c) \(\frac{7}{20}\)
(d) \(\frac{13}{20}\)
Answer:
(c) \(\frac{7}{20}\)
Total Balls = 5 + 8 + 7 = 20
∴ P (neither a blue nor a pink ball)
= 1 – (\(\))
= 1 – (\(\frac{8+5}{20}\)) =1 – \(\frac{13}{20}\) = \(\frac{7}{20}\)

Question 12.
The volume of a right circular cone whose area of the base is 156 cm2 and the vertical height is 8 cm, is 1
(a) 2496 cm ³
(b) 1248 cm ³
(c) 1664 cm ³
(d) 416 cm ³
Answer:
(d) 416 cm ³
Volume of cone
= \(\frac{1}{3}\) × (Area of Base) × height
= \(\frac{1}{3}\) × 156 × 8 = 416 cm ³

Question 13.
3 chairs and 1 table cost ₹900, whereas 5 chairs and 3 tables cost ₹2,100. If the cost of 1 chair is ₹ x and the cost of 1 table is ₹ y, then the situation can be represented algebraically as 1
(a) 3x + y = 900, 3x + 5y = 2100
(b) x + 3y = 900, 3x + 5y = 2100
(c) 3x + y = 900,5x + 3y = 2100
(d) x + 3y = 900, 5x + 3y = 2100
Answer:
(c) 3x + y = 900,5x + 3y = 2100
3x + 1y = ₹900
5x + 3y = ₹2100

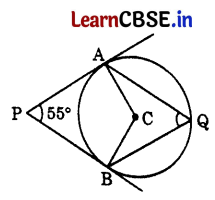
Question 14.
In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is 1

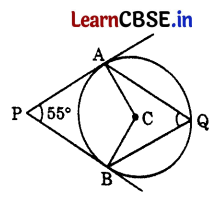
(a) 621/2°
(b) 125°
(c) 55°
(d) 90°
Answer:
(a) 621/2°
AC & BC are radii and PA and PB are tangents.
∠PAC = ∠PBC = 90° …[Tangent is ⊥ to the radius through the point of contact
In quad. PACB,
55° + 90° + ∠ACB + 90° = 360° …[Angle-sum-property of a quadrilateral
⇒ ∠ACB = 360° – 235° = 125°
Now, ∠AQB = ∠ACB
= \(\frac{125}{2}\) = 62\(\frac{1}{2}\)° ….[The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of circle.

Question 15.
A card is drawn at random from a well shuffled deck of 52 playing cards. 1
The probability of getting a face card is
(a) \(\frac{1}{2}\)
(b) \(\frac{3}{13}\)
(c) \(\frac{4}{13}\)
(d) \(\frac{1}{13}\)
Answer:
(b) \(\frac{3}{13}\)

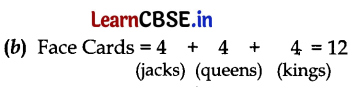
∴ P (Face Card) = \(\frac{12}{52}\) = \(\frac{3}{13}\)

Question 16.
If θ is an acute angle of a right angled triangle, then which of the following equations is not true? 1
(a) sin θ cot θ = cos θ
(b) cos θ tan θ = sin θ
(c) cosec ² θ – cot ² θ = 1
(d) tan ² θ – sec ² θ = 1
Answer:
(d) tan ² θ – sec ² θ = 1
Identity: sec ² θ – tan ² θ = 1
so, tan ² θ – sec ² θ ≠ 1

Question 17.
If the zeroes of the quadratic polynomial x ² + (a + 1) x + b are 2 and -3, then 1
(a) a = -7, b = -1
(b) a = 5, b = -1
(c) a = 2, b = -6
(d) a = 0, b = -6
Answer:
(d) a = 0, b = -6
Given. Zeroes of quadratic polynomial,
x ² + (a + 1) x + b
α = 2 and β = -3
Here, A = 1, B = a + 1, C = b
∴ Sum of 0 = \(\frac{-B}{A}\)
⇒ 2 + (-3) = \(\frac{-(a+1)}{1}\)
⇒ -1 = -(a + 1)
∴ a = 1 – 1 = 0

∴ Product of 0 = \(\frac{C}{A}\)
⇒ 2(-3) = \(\frac{b}{1}\)
∴ b = -6

Question 18.
If the sum of the first n terms of an A.P be 3n ² + n and its common difference is 6, then its first term is 1
(a) 2
(b) 3
(c) 1
(d) 4
Answer:
(d) 4
S _n = 3n ² + n …[Given
Put n = 1, S ₁ = 3(1) ² + 1 = 3 + 1= 4
∴ First term = a = S ₁ = 4

Assertion – Reason Based Questions: In question numbers 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R).

Choose the correct option out of the following:
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true and R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is False but R is true.

Question 19.
Assertion (A): If 5 + √7 is a root of a quadratic equation with rational co-efficients, then its other root is 5 – √7
Reason (R): Square roots of a quadratic equation with rational co-efficients occur in conjugate pairs.
Answer:
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).

Question 20.
Assertion (A): For 0 < θ ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other. 1
Reason (R): cosec ² θ – cot ² θ = 1.
Answer:
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(cosec θ – cot θ) × (cosec θ + cot θ)
= cosec ² θ – cot ² θ
= 1 R is True.

Section – B

Section B consists of Very Short Answer (VSA) type of questions of 2 marks each.

Question 21.
(a) Show that 6 ⁿ cannot end with digit 0 for any natural number ‘n’. 2
Or
(b) Find the HCF and LCM of 72 and 120.
Answer:
(a) If the number 6 ⁿ , for any n, were to end with the digit zero, then it would be divisible by 5. That is, the prime factorisation of 6 ⁿ will contain the prime number 5. This is not possible because Prime factorisation of 6 ⁿ does not contain 5 as a factor.
6 ⁿ = (2 × 3) ⁿ = 2 ⁿ × 3 ⁿ
So, there is no natural number (n) for which 6″ ends with the digit zero.
Or
(b) 72 = 2 ³ × 3 ²
120 = 2 ³ × 3 × 5
∴ HCF = 2 ³ × 3 ¹
= 24

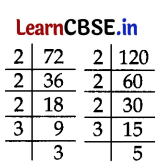
∴ LCM = 2 ³ × 3 ² × 5 = 360

Question 22.
A line intersects y-axis and x-axis at point P and Q respectively. If R(2, 5) is the mid-point of line segment PQ, then find the coordinates of P and Q. 2
Answer:
Let P (0, y) and Q (x, 0).
Mid point of PQ = R
(\(\frac{0+x}{2}, \frac{y+0}{2}\)) (2, 5) …[mid-point theorem
⇒ \(\frac{x}{2}\) = 2
⇒ x = 4

⇒ \(\frac{y}{2}\) = 5
⇒ y = 10
∴ Coordinates of P (0, y) = (0, 10)
Coordinates of Q (x, 0) = (4, 0)

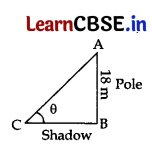
Question 23.
Find the length of the shadow on the ground of a pole of height 18 m when angle of elevation θ of the sun is such that tan θ = \(\frac{6}{7}\).
Answer:
In a ΔABC, tan θ = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ \(\frac{6}{7}\) = \(\frac{18}{B C}\) …[ tan θ = \(\frac{6}{7}\) …[Given
⇒ 6 BC = 18 × 7
∴ Length of shadow, BC = \(\frac{18 \times 7}{6}\) = 21 m

Question 24.
In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter.
If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle. 2

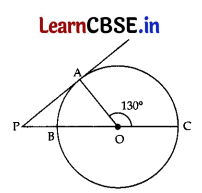
Answer:

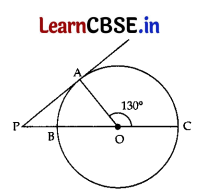
Given. OA is the radius and PA is the tangent.
⇒∠PAO = 90° …[Tangent is ⊥ to the radius through the point of contact
∴ ∠APO + ∠PAO = ∠AOC …[Exterior angle theorem
⇒ ∠APB + 90° = 130°
∴ ∠APB = 130° – 90° = 40°

Question 25.
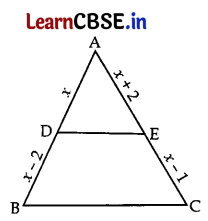
(a) In the given figure, ABC is a triangle in which DE || BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then find the value of x. 2

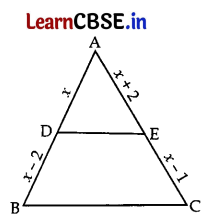
Or
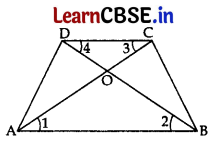
(b) Diagonals AC and BD of trapezium ABCD with AB || DC intersect each other at point O. Show that
\(\frac{\mathrm{OA}}{\mathrm{OC}}\) = \(\frac{\mathrm{OB}}{\mathrm{OD}}\)

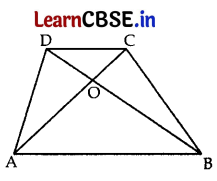
Answer:
(a) In ΔABC, DE || BC
∴ \(\frac{\mathrm{AD}}{\mathrm{BD}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\) …[Thales’ theorem
⇒ \(\frac{x}{x-2}=\frac{x+2}{x-1}\)
⇒ x (x – 1) = (x – 2) (x + 2)
⇒ x ² – x = x ² – 4
∴ x = 4 units

(b) In ΔAOB and ΔCOD,
AB || CD …[Given
∠1 = ∠3 …[Alternate interior angles
∠2 = ∠4
∴ ΔAOB ~ ΔCOD …[By AA corollary
\(\frac{\mathrm{BO}}{\mathrm{DO}}\) = \(\frac{\mathrm{AO}}{\mathrm{CO}}\) ……[In similar Δs corresponding sides are proportional.
∴ \(\frac{\mathrm{OA}}{\mathrm{OC}}\) = \(\frac{\mathrm{OB}}{\mathrm{OD}}\) (Hence proved)

Section – C

Section C consists of Short Answer (SA) type of questions of 3 marks each.

Question 26.
Find the ratio in which the line segment joining the points A(6, 3) and B(-2, -5) is divided by x-axis. 3
Answer:

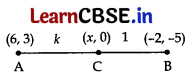
Let C (x, 0) be any point on x-axis.
Let AC : CB = m ₂ : m ₁ = k : 1
Using section formula, \(\frac{-5 k+3}{k+1}=\frac{0}{1}\)
⇒ -5k + 3 = 0 ⇒ -5k = -3
∴ k = \(\frac{3}{5}\)
∴ Required Ratio = k : 1 = \(\frac{3}{5}\) : 1 or = 3 : 5

Question 27.
(a) Find the HCF and LCM of 26, 65 and 117, using prime factorisation. 3
Or
(b) Prove that √2 is an irrational number.
Answer:
(a) Prime factorisation of 26 = 2 × 13
65 = 5 × 13
117 = 3 ² × 13
∴ HCF = 13
LCM = 2 × 5 × 3 ² × 13 = 1170
Or
(b) Let us assume, to the contrary, that √2 is rational. That is, we can find integers a
and b (≠ 0) that √2 = \(\frac{a}{b}\).
Suppose a and b have a common factor other than 1, then we can divide by the common factor and assume that a and b are coprime.
So, b√2 = a
Squaring on both sides, & rearranging, we get 2b ² = a ² Therefore, a ² is divisible by 2 and a is also divisible by 2. So, we can write a = 2c for some integer c. Substituting for a, we get 2b ² = 4c ² , that is b ² = 2c ² .

This means that b2 is divisible by 2 and so b is also divisible by 2. Therefore, a and b have at least 2 as a common factor. But this contradicts the fact that a and b are coprime.

This contradiction has arisen because of our incorrect assumption that √2 is rational.
So we conclude that √2 is irrational.

Question 28.
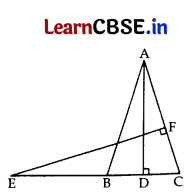
In the given figure, Eisapoint on the side CB produced of anisosceles triangle ABC with AB = AC. If AD⊥BC and EF⊥ AC, then prove that triangle ΔABD ~ ΔECF. 3

Answer:

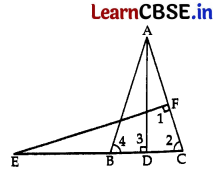
In ΔABC, AB = AC …[Given
∴ ∠4 = ∠2 …(i) [Angles opposite equal sides
In ΔABD and ΔECF,
∠3 = ∠1 …[Each 90°
∠4 = ∠2 …[From (i)
∴ ΔABD ~ ΔECF …[AA similarity criterion

Question 29.
(a) The sum of two numbers is 15. If the sum of their reciprocals is \(\frac{3}{10}\), find the two numbers. 3
Or
(b) If α and β are roots of the quadratic equation x ² – 7x + 10 = 0, find the quadratic equation , whose roots are α ² and β ² . 3
Answer:
(a) Let two numbers be x and 15 – x. According to question,
⇒ \(\frac{1}{x}+\frac{1}{15-x}=\frac{3}{10}[latex] ⇒ [latex]\frac{15-x+x}{x(15-x)}=\frac{3}{10}[latex]
⇒ 150 = 3x(15 – x) ⇒ 50 = 15x – x ²
⇒ x ² – 15x + 50 = 0
⇒ x ² – 10x – 5x + 50 = 0
⇒ x(x – 10) -5 (x – 10) = 0
⇒ (x – 5) (x – 10) = 0
⇒ x – 5 = 0 or x – 10 = 0
⇒ x = 5 or x = 10
When x = 5, numbers are 5, 10
When x = 10, numbers are 10, 5
Or
(b) Given, x ² – 7x + 10 = 0
a = 1, b = -7, c = 10
Sum of roots, α + β = [latex]\frac{-b}{a}=\frac{-(-7)}{1}\) = 7 …(i)
Product of roots, αβ = \(\frac{c}{a}\) = 10 …(ii)
For required Polynomial,
Sum of roots, S = α ² + β ² = (α + β) ² – 2αβ
= (7) ² – 2(10) …[From (i) and (ii)
= 49 – 20 = 29
Product of roots, P = α ² β ²
= (αβ) ² …[From (ii)
= (10) ² = 100
∴ Required Quadratic Polynomial,
x ² – Sx + P = 0 ∴ x ² – 29x + 100 = 0

Question 30.
Prove that: \(\frac{1+\sec A}{\sec A}=\frac{\sin ^2 A}{1-\cos A}\) 3
Answer:

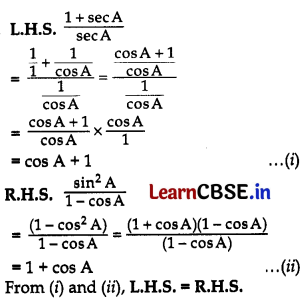
Question 31.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the sector formed by the arc. Also, find the length of the arc. 3
Answer:

Here r = 21 cm, θ = 60°
Area of sector = \(\frac{\theta}{360^{\circ}}\)πr ²
= \(\frac{60^{\circ}}{360^{\circ}}\) × \(\frac{22}{7}\) × 21 × 21
= 231 cm ²
Length of an arc = \(\frac{\theta}{360^{\circ}}\) (2πr)
= \(\frac{60^{\circ}}{360^{\circ}}\) × 2 × \(\frac{22}{7}\) × 21 = 22 cm

Section – D

Section D Consists of Long Answer (LA) type questions of 5 marks each.

Question 32.
(a) Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2 ∠OPQ. 5

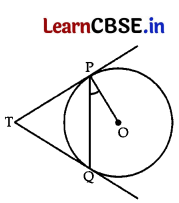
Or
(b) A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively.
Show that AQ = \(\frac{1}{2}\) (Perimeter of ΔABC).

Answer:
(a) Given. A circle with centre O, an external point T and two tangents TP and TQ to the circle, where P, Q are the points of contact.

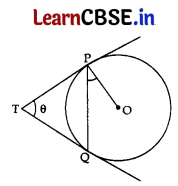
To Prove. ∠PTQ = 2∠OPQ
Proof: Let ∠PTQ = θ
Now, TP = TQ ……[∵ Lengths of tangents drawn from an external Point to a circle are equal
So, TPQ is an isosceles triangle
∴ ∠TPQ = ∠TQP = \(\frac{1}{2}\) (180° – θ)
= 90° – \(\frac{1}{2}\)θ …….. (i)
Also, ∠OPT = 90° ……[∵Tangent at any point of a circle is⊥to radius through the pt. of contact
So, ∠OPQ = ∠OPT – ∠TPQ = 90° – (90° – \(\frac{1}{2}\) θ) …….[From (i)
∠OPQ = \(\frac{1}{2}\) θ ⇒ ∠OPQ = \(\frac{1}{2}\) ∠PTQ
∴ ∠PTQ = 2∠OPQ (Hence Proved)
Or
(b) Since the tangents from an external point to a circle are equal in length.

Now, Perimeter of ΔABC = AB + BC + AC
= AQ – BQ + BP + PC + AR – CR
= AQ – BP + BP + CR + AQ – CR …[Using (i), (ii) and (iii)
∴ Perimeter of ΔABC = 2AQ
AQ = \(\frac{1}{2}\) (Perimeter of ΔABC)
(Hence Proved)

Question 33.
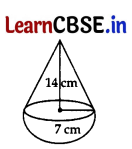
A solid is in the shape of a right-circular cone surmounted on a hemisphere, the radius of each of them being 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid. 5
Answer:
Given, r = 7 cm, h = 2r = 14 cm
Vol. of solid = Vol. of cone + Vol. of hemisphere
= \(\frac{1}{3}\)πr ² h + \(\frac{2}{3}\)πr ³ = \(\frac{1}{3}\) πr ² (h + 2r)
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 7 × 7 (14 + 14)
= \(\frac{22 \times 7 \times 28}{3}\) \(\frac{4312}{3}\)
= 1437.3 cm ³

Question 34.
(a) The ratio of the 11th term to the 18th term of an AP is 2 : 3. Find the ratio of the 5th term to the 21st term. Also, find the ratio of the sum of first 5 terms to the sum of first 21 terms. 5
Or
(b) If the sum of first 6 terms of an AP is 36 and that of the first 16 terms is 256, find the sum of first 10 terms.
Mass (in grams) 80-100 100-120 120-140 140-160 160-180
Number of apples 20 60 70 X 60
Answer:
(a) \(\frac{a_{11}}{a_{18}}\) = \(\frac{2}{3}\) …[Given
\(\frac{a+10 d}{a+17 d}\) = \(\frac{2}{3}\) …[∵ a _n = a + (n – 1)d
⇒ 3a + 30d = 2a + 34 d
⇒ 3a – 2a = 34d + -30d
a = 4d …… (i)

Or
(b) Given. S ₆ = 36
⇒ \(\frac{6}{2}\)(2a + 5d) = 36 … [∵ S _n = \(\frac{n}{2}\)(2a + (n – 1 )d
⇒ 2a + 5d = 12 ⇒ 2a = 12 – 5d ……. (i)
and S ₁₆ 256 …..[Given
⇒ \(\frac{16}{2}\) (2a + 15d) = 256
⇒ 2a + 15d = \(\frac{256}{2}\)
⇒ 12 – 5d + 15d = 32 …..[From (i)
10d = 32 – 12
∴ d \(\frac{20}{10}\) = 2
From (i), 2a = 12 – 5(2)
⇒ 2a = 2 :. a = 1
As we know, S _n = \(\frac{n}{2}\) [2a + (n – 1)d]
∴ S ₁₀ = \(\frac{10}{2}\)(2a + 9d)
= 5 (2(1) + 9(2))
= 5 (2 + 18) = 5 (20) = 100

Question 35.
250 apples of a box were weighed and the distribution of masses of the apples is given in Find the value of x and the mean mass of the apples.

(ii) Find the modal mass of the apples.
Answer:

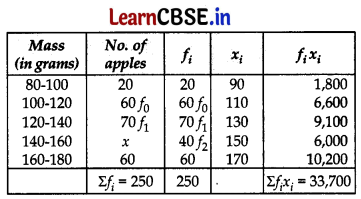
Total Apples = 250 …..[Given
⇒ 20 + 60 + 70 + x + 60 = 250
⇒ 210 + x = 250
∴ x = 250 – 210 = 40
(i) Mean Mass = \(\frac{\Sigma f_i x_i}{\Sigma f_i}\)
= \(\frac{33700}{250}\) = 134.8 gms

(ii) Since Maximum Frequency is 70
So Modal class in 120 – 140
∴ Modal mass = l + \(\frac{f_1-f_0}{2 f_1-f_0-f_2}\) × h ..[Here, l = 120, f ₀ = 60, f ₁ = 70, f ₂ = 40, h = 20
= 120 + \(\frac{70-60}{140-60-40}\) × 20
= 120 + \(\frac{10 \times 20}{40}\)
h = 20
= 120 + 5 = 125 gms

Section – E

3 Case Study Based Questions. Each question is of 4 marks.

Question 36.
A coaching institute of Mathematics conducts classes in two batches I and II and fees for rich and poor children are different. In batch I, there are 20 poor and 5 rich children, whereas in batch II, there are 5 poor and 25 rich children. The total monthly collection of fees from batch I is ₹9000 and ‘from batch II is ₹26,000. Assume that each” poor child
pays ₹ x per month and each rich child pays ₹ y per month.

Based on the above information, answer the following questions :
(i) Represent the information given above in terms of x and y. 1
(ii) Find the monthly fee paid by a poor child. 2
Or
Find the difference in the monthly fee paid by a poor child and a rich child. 2
(iii) If there are 10 poor and 20 rich children in batch III, what is the total monthly collection of fees from batch III? 1
Answer:
(i) A.T.Q. 20x + 5y = 9,000 ……(A)
5x + 25 y = 26,000 …….(B)

(ii) Multiplying (A) by 1 and (B) by \(\frac{1}{5}\) we have

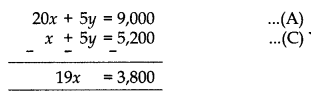
∴ x = \(\frac{3800}{19}\) = ₹200
From (C), 200 + 5y = 5200
⇒ 5y = 5200 – 200
∴ y = \(\frac{5000}{5}\) = ₹1,000
∴ Monthly fee paid by a poor child x = ₹200
∴ Required difference = y – x
= ₹(1,000 – 200) = ₹800

(iii) Total collection of Fees from Batch III
= 10x + 20y
= 10(200) + 20(1,000) …[From Point (ii)
= 2,000 + 20,000 = ₹22,000

Question 37.
Radio towers are used for transmitting a range of communication services including radio and television. The tower will either act as an antenna itself or support one or more antennas on its structure. On a similar concept, a radio station tower was built in two Sections A and B. Tower is supported by wires from a point O.

Distance between the base of the tower and point O is 36 cm. From point O, the angle of elevation of the top of the Section B is 30° and the angle of elevation of the top of Section A is 45°.

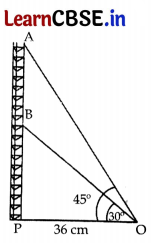
Based on the above information, answer the following questions :
(i) Find the length of the wire from the point O to the top of Section B. 1
(ii) Find the distance AB. 2
Find the area of ΔOPB,
(iii) Find the height of the Section A from the base of the tower. 1
Answer:

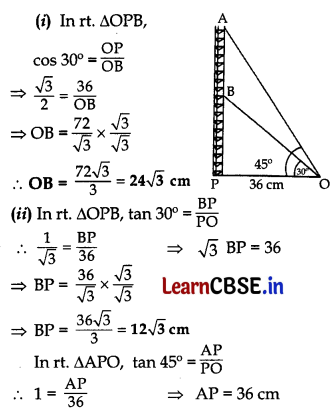
∴ AB = AP – BP = 36 – 12√3
= 12(3 – √3)cm or 12√3(√3 – 1) cm
Or
ar. (ΔOPB) = \(\frac{1}{2}\) × Base × height
= \(\frac{1}{2}\) × PO × PB
= \(\frac{1}{2}\) × 36 × 12√3
= 216√3 cm ³

(iii) From (ii) above AP = 36 cm
Alternatively, AP = AB + BP
AP = AB + BP
= 12√3(√3 – 1) + 12√3
= 36 – 12√3 + 12√3 = 36 cm

Question 38.
“Eight Ball” is a game played on a pool table with 15 balls numbered 1 to 15 and a “cue ball” that is solid and white. Of the 15 numbered balls, eight are solid (non-white) coloured and numbered 1 to 8 and seven are striped balls numbered 9 to 15.

The 15 numbered pool balls (no cue ball) are placed in a large bowl and mixed, then one ball is drawn out at random.

Based on the above information, answer the following questions :
(i) What is the probability that the drawn ball bears number 8? 1
(ii) What is the probability that the drawn ball bears an even number? 2
What is the probability that the drawn ball bears a number, which is a multiple of 3?
(in) What is the probability that the drawn ball is a solid coloured and bears an even number? 1
Answer:
Non-White balls = 8 (nos. 1 to 8)
Striped balls = 7 (nos. 9 to 15)
White solid cue ball = 1
Total number of balls = 8 + 7 = 15

(i) P(number 8 ball) = \(\frac{1}{15}\) …[There is one eight number ball

(ii) Even balls 2,4, 6,8,10,12,14 i.e 7 balls 7
∴ P(even number) = \(\frac{7}{15}\)
Or
“Multiples of 3” are 3, 6, 9, 12, 15 i.e 5 balls
∴ P(multiple of 3) = \(\frac{5}{15}\) = \(\frac{1}{3}\)

(iii) Solid coloured and bear even number balls are 2, 4, 6, 8 i.e 4 balls
∴ Required probability = \(\frac{4}{15}\)

SET Code No. 30/6/2

Note: Except for the following questions, all the remaining questions have been asked in Set – I.

Question 6.
The LCM of smallest 2-digit number and smallest composite number is 1
(a) 12
(b) 4
(c) 20
(d) 40
Answer:
(c) 20
Smallest 2 digit number = 10 = 2 × 5
Smallest composite number = 4 = 2 ²
∴ LCM (10,4) = 2 ² × 5 = 20

Question 7.
The distance of the point (-4, 3) from y-axis is 1
(a) -4
(b) 4
(c) 3
(d) 5
Answer:
(b) 4
Distance of (-4, 3) from y-axis is 4.
Note : Distance is not negative.

Question 8.
If one zero of the polynomial x ² + 3x + k is 2, then the value of k. 1
(a) -10
(b) 10
(c) 5
(d) -5
Answer:
(a) -10
Let P(x) = x ² + 3x + k
∴ x = 2 …[ ∵ 2 is a zero of P(x)
⇒ (2) ² + 3(2) + k = 0
⇒ 4 + 6 + k = 0 ∴ k = -10

Question 16.
A box contains 90 discs, numbered from 1 to 90. If one disc is drawn at random from the box, the probability that it bears a prime number less than 23 is 1
(a) \(\frac{7}{90}\)
(b) \(\frac{1}{9}\)
(c) \(\frac{4}{45}\)
(d) \(\frac{9}{89}\)
Answer:
(c) \(\frac{4}{45}\)
Let x be the Prime number less than 23 Such numbers are 2, 3, 5, 7, 11, 13, 17, 19 i.e 8
∴ P(x) = \(\frac{8}{90}\) = \(\frac{4}{45}\)

Question 17.
The coordinates of the point where the line 2y = 4x + 5 crosses ar-axis is 1
(a) (o, \(\frac{-5}{4}\))
(b) (o, \(\frac{5}{2}\))
(c) (\(\frac{-5}{4}\), 0)
(d) (\(\frac{-5}{2}\), o)
Answer:
(c) (\(\frac{-5}{4}\), 0)
Given. 2y = 4x + 5
∴ 2(0) – 5 = 4x …[To cut x-axis, y = 0
∴ x = \(\frac{-5}{4}\)
∴ Point (x, y) = (\(\frac{-5}{4}\), 0)

Question 18.
(cos ⁴ A – sin ⁴ A) on simplification, gives 1
(a) 2 sin ² A – 1
(b) 2 sin ² A + 1
(c) 2 cos ² A + 1
(d) 2 cos ² A – 1
Answer:
(d) 2 cos ² A – 1
Given, cos ⁴ A – sin ⁴ A
= (cos ² A) ² – (sin ² A) ²
= (cos ² A – sin ² A) (cos ² A + sin ² A)
= [(cos ² A – (1 – cos ² A)]. (1)
= [(cos ² A – 1 + cos ² A]. 1 = 2 cos ² A – 1

Question 24.
Find the points on the x-axis, each of which is at a distance of 10 units from the point A(11, -8). 2
Answer:
Let B(x, 0) be any point on x-axis.
AB = 10 units …[Given
(AB) ² = 100 …[Squaring both sides
⇒ (x – 11) ² + (0 + 8) ² = 100
⇒ (x – 11) ² + 64 = 100
⇒ (x – 11) ² = 100 – 64
⇒ (x – 11) ² = 36
⇒ x – 11 = ±6 …[Taking Square-root on both sides
⇒ x = 11 ±6
⇒ x = 11 + 6 or x = 11 – 6
∴ x = 17 or x = 5
∴ B = (17, 0) or (5,0)

Question 26.
In the given figure, AB and CD are diameters of a circle with centre O perpendicular to each other. If OA = 7 cm, find the area of shaded region. 3

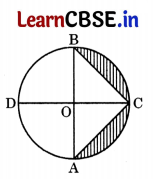
Answer:
Area of shaded region
= Area of Semi-circle – Ar. (ΔABC)
= \(\frac{1}{2}\)πr ² – \(\frac{1}{2}\) × AB × OC
= \(\frac{1}{2}\) × \(\frac{22}{7}\) × 7 × 7 – \(\frac{1}{2}\) × 14 × 7 [∵ AB = 7 + 7 = 14cm OC = r = 7 cm ]
= 77 – 49 = 28 cm ²

Question 27.
If sin θ + cos θ = p and sec θ + cosec θ = q, then prove that q(p ² – 1) = 2p. 3
Answer:
We have, p = sin θ + cos θ
q = sec θ + cosec θ
L.H.S. q (p ² – 1)
= (sec θ + cosec θ) [(sin θ + cos θ) ² – 1]
= (\(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\)) (sin ² θ + cos ² θ + 2sin θ cos θ – 1)
= (\(\frac{\sin \theta+\cos \theta}{\cos \theta \sin \theta}\)) (2 sin θ cos θ)…[∵ sin ² θ + cos ² θ = 1
= 2 (sin θ + cos θ)
= 2p = R.H.S (Hence Proved)

Question 34.
A solid is in the shape of a right-cirular cone surmounted on a hemisphere, the radius of each of them being 3.5 cm and the total height of the solid is 9.5 cm. Find the volume of the soild. 5
Answer:

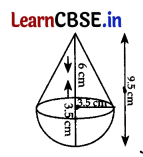
r = 3.5 cm or \(\frac{7}{2}\) cm
Height of cone, h =9.5 – 3.5
= 6 cm
∴ Vol. of solid = Vol. of cone + Vol. of hemisphere
= \(\frac{1}{2}\) πr ² h + \(\frac{2}{3}\) πr ³
= \(\frac{1}{2}\) πr ² (h + 2r)
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) × (6 + 2 × \(\frac{7}{2}\))
= \(\frac{77}{3}\) × 13 = \(\frac{1001}{6}\) = \(166.8 \overline{3}\) cm ³

Question 35.
(a) Find the sum of integers between 100 and 200 which are 5
(i) divisible by 9
(ii) not divisible by 9.
Or
(b) Solve the equation : -4 + (-1) + 2 + 5 + ………. + x = 437.
Answer:
(a) (i) Nos. divisible by 9 between 100 & 200 are
108, 117, 126, ………… a _n
Here a = 108, d = 117 – 108 = 9, a _n – 198
∴ a + (n – 1) d = a _n
⇒ 108 + (n – 1) 9 = 198
⇒ (n – 1)9 = 198 – 108
⇒ (n – 1) = \(\frac{90}{9}\) ∴ n = 11
Now, S _n = \(\frac{n}{2}\) (a ₁ + a _n )
S ₁₁ = \(\frac{11}{2}\) (108 + 198)
= \(\frac{11}{2}\) × 306 = 11 × 153 = 1683

(ii) Let S be the sum of integers between 100 and 200.
∴ S = 101 + 102 + 103 + ………… + 199
Here a ₁ = 101, a _n = 199,
n = 199 – 101 + 1 = 99
∴ S = \(\frac{99}{2}\) (101 + 199)
= \(\frac{99}{2}\) (300) = 99 × 150 = 14,850
Now, Sum not divisible by 9 = 14850 – 1683 = 13167
Or
(b) Here, a = -4, d = -1 – (-4) = 3, a _n = x
Given. S _n = 437
∴ \(\frac{n}{2}\) [2a + (n – 1) (d)] = 437
⇒ \(\frac{n}{2}\) [2 (-4) + (n – 1)(3)] = 437
⇒ n (-8 + 3n – 3) = 874
⇒ n (3n – 11) = 874
⇒ 3n ² – 11n – 874 = 0
⇒ 3n ² – 57n + 46n – 874 = 0
⇒ 3n(n – 19) + 46 (n – 19) = 0
⇒ (n – 19) (3n + 46) = 0
⇒ n – 19 = 0 or 3n + 46 = 0
∴ n = 19 or n = \(\frac{-46}{3}\) (Not possible) …[n must be a rational number
Now, x = a _n
x = a + (n – 1)d
= -4 + (19 – 1)(3) = -4 + 54 = 50
*Note: 2 ^nd Method using x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)

SET III Code. 30/6/3

Note: Except for the following questions, all tire remaining questions have been asked in Set – I and Set II.

Question 1.
The distance between the points (0, 5) and (-3, 1) is :
(a) 8 units
(b) 5 units
(c) 3 units
(d) 25 units
Answer:
(b) 5 units
Given. A (0, 5) and B (-3, 1)
∴ AB = \(\sqrt{(-3-0)^2+(1-5)^2}\) …[Using distance formula
= \(\sqrt{9+16}\) = \(\sqrt{25}\) = 5 units

Question 2.
If tan θ = \(\frac{x}{y}\), then cos θ is equal to
Answer:
(a) \(\frac{x}{\sqrt{x^2+y^2}}\)
(b) \(\frac{y}{\sqrt{x^2+y^2}}\)
(c) \(\frac{x}{\sqrt{x^2-y^2}}\)
(d) \(\frac{y}{\sqrt{x^2-y^2}}\)
Answer:
(b) \(\frac{y}{\sqrt{x^2+y^2}}\)
Given, tan θ = \(\frac{x}{y}\)
As we know, sec ² θ = 1 + tan ² θ
sec ² θ = 1 + \(\frac{x^2}{y^2}\)
⇒ sec ² θ = \(\frac{y^2+x^2}{y^2}\)
⇒ sec θ = \(\sqrt{\frac{x^2+y^2}{y^2}}=\frac{\sqrt{x^2+y^2}}{y}\)
∴ cos θ = \(\frac{1}{\sec \theta}=\frac{y}{\sqrt{x^2+y^2}}\)

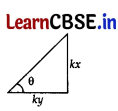
Alternatively, tan θ = \(\frac{x}{y}=\frac{\mathrm{P}}{\mathrm{B}}\)
In rt. Δ, H ² = P ² + B ²
= k ² x ² + k ² y ² …[Pythagoras’ theorem
⇒ H ² = k ² (x ² + y ² )
⇒ H = k\(\sqrt{x^2+y^2}\)
∴ cos θ \(\frac{\mathrm{B}}{\mathrm{H}}=\frac{k y}{k \sqrt{x^2+y^2}}=\frac{y}{\sqrt{x^2+y^2}}\)

Question 3.
The zeroes of the polynomial 3x ² + 11x -4 are:
(a) \(\frac{1}{3}\), -4
(b) \(\frac{-1}{3}\), 4
(c) \(\frac{1}{3}\), 4
(d) \(\frac{-1}{3}\), 4
Answer:
(a) \(\frac{1}{3}\), -4
Given. 3x ² + 11x – 4
⇒ 3x ² + 12x – x – 4
⇒ 3x (x + 4) – 1(x + 4)
⇒ (x + 4) (3x – 1)
∴ Zeroes are: x + 4 = 0 or 3x – 1 = 0
x = -4 or x = 1/3

Question 16.
If ‘p’ is a root of the quadratic equation x ² – (p + q) x + k = 0 then the value of ‘k’ is
(a) p
(b) q
(c) p + q
(d) pq
Answer:
(d) pq
Given. x ² – (p + q)x + k = 0
Since p is one of the root, …[Given
∴ p ² – (p + q)p + k = 0
⇒ p ² – p ² – pq + k = 0 ∴ k = pq

Question 17.
Cards bearing numbers 3 to 20 are placed in a bag and mixed thoroughly. A card is taken out of the bag at random. What is the probability that the number on the card taken out is an even number? 1
(a) \(\frac{9}{17}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{5}{9}\)
(d) \(\frac{7}{18}\)
Answer:
(b) \(\frac{1}{2}\)
We have, 3, 4, 5 ………….. 20
Total cards = 18
Even number cards are 4, 6, 8, 10, 12, 14, 16, 18, 20 i.e., 9
∴ P(even numbers) = \(\frac{9}{18}\) = \(\frac{1}{2}\)

Question 18.
The condition for the system of linear equations ax + by = c; lx + my = n have a unique solution is 1
(a) am ≠ bl
(b) al ≠ bm
(c) al = bm
(d) am = bl
Answer:
(a) am ≠ bl
Given, ax + by = c
lx + my = n
For unique solution: \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
\(\frac{a}{l} \neq \frac{b}{m}\)
∴ am ≠ bl

Question 21.
Find the ratio in which the y-axis divides the line segment joining the points (5, -6) and (-1, -4). 2
Answer:
Let C(0,y) be any point on y-axis.

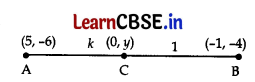
Let AC : CB = k : 1
Coordinates of C = Coordinates of C
\(\frac{-k+5}{k+1}, \frac{-4 k-6}{k+1}\) = (0, y) ..[Using formula
⇒ \(\frac{-k+5}{k+1}\) = 0 ⇒ -k + 5
∴ k = 5
∴ Required Ratio = k : 1 = 5: 1

Question 26.
Prove that (sin θ + cos θ) (tan θ + cot θ) = sec θ + cosec θ. 3
Answer:
L.H.S = (sin θ + cos θ) (tan θ + cot θ)
= (sin θ + cos θ) (\(\frac{\sin \theta}{\cos \theta}+\frac{\cos \theta}{\sin \theta}\))
= (sin θ + cos θ) (\(\frac{\sin ^2 \theta+\cos ^2 \theta}{\cos \theta \sin \theta}\))
= \(\frac{\sin \theta+\cos \theta}{\sin \theta \cos \theta}\) ….[∵ sin ² θ + cos ² θ = 1
\(\frac{\sin \theta}{\sin \theta \cos \theta}+\frac{\cos \theta}{\sin \theta \cos \theta}\)
= sec θ+ cosec θ = R.H.S (Hence Proved)

Question 27.
(a) A natural number, when increased by 12, equals 160 times its reciprocal. Find the number. 3
Or
(b) If one root of the quadratic equation x ² + 12x – k = 0 is thrice the other root, then find the value of k.
Answer:
(a) Let the number be x.
A.T.Q., (x + 12) = 16o(\(\frac{1}{x}\))
x (x + 12) = 160
⇒ x ² + 12x – 160 = 0
⇒ x ² + 20x – 8x – 160 = 0
⇒ (x – 8) (x + 20) = 0
⇒ x – 8 = 0 or x + 20 = 0
⇒ x = 8 or x = -20 (not possible)
Natural number must be positive
∴ Required number, x = 8.
Or
(b) Given, x ² + 12x + k = 0. Let roots be α and 3α
Here a = 1, b = 12, c = -k
Sum of roots = \(\frac{-b}{a}\)
α + 3α = \(\frac{-12}{1}\)
4α = -12
∴ α = -3 ….. (i)

Product of roots = \(\frac{c}{a}\)
α(3α) = \(\frac{-k}{1}\)
3α ² = -k
3(-3) ² = -k ….[From (i)
∴ k = -27

Question 32.
(a) The sum of first seven terms of an A.P. is 182. If its 4 ^th term and the 17 ^th term are in the ratio 1: 5, find the A.P. 5
Or
(b) The sum of first q terms of an A.P. is 63q – 3q ² . If its p ^th term is – 60, find the value of p. Also, find the 11 ^th term of this A.P.
Answer:
(a) S ₇ = 182
⇒ \(\frac{7}{2}\) (2a + 6d) = 182 …[∵ S _n = \(\frac{n}{2}\) (2a + (n – 1)d
⇒ (a + 3d) = \(\frac{182}{7}\) ⇒ a + 3d = 26
⇒ a = 26 – 3d …… (i)

From (i), a = 26 – 3 (8) = 26 – 24 = 2
∴ AP is a, a + d, a + 2d, a + 3d, 2, 10, 18, 26..
Or
(b) Given. Sq = 63q – 3q ²
Put q = 1, S ₁ = 63(1) – 3(1) ² = 63 – 3 = 60
Put q = 2, S ₂ = 63(2) – 3(2) ² = 126 – 12 = 114
a ₁ = S ₁ = 60
a ₂ = S ₂ – S ₁ = 114 – 60 = 54
d = a ₂ – a ₁
= 54 – 60 = -6
Now, a _p = -60
⇒ a + (p – 1 )d = -60 …[∵ a = a ₁ = 60
⇒ 60 + (p – 1)(-6) = -60
⇒ (p -1 )(-6) = -60 – 60
⇒ P – 1 = \(\frac{-120}{-6}\)
∴ p = 20 + 1 = 21
Now, a ₁₁ = a + 10d = 60 + 10(-6) = 60 – 60 = 0

Question 33.
(a) Prove that a parallelogram circumscribing a circle is a rhombus. 5
Or
(b) In the given figure, tangents PQ and PR are drawn to a circle such that ∠RPQ 30°. A chord RS is drawn parallel to the tangent PQ. Find the measure of ∠RQS.

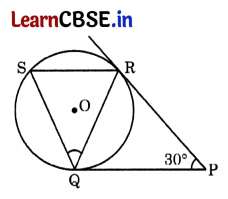
Answer:
(a)

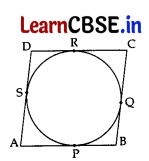
Given. ABCD is a || ^gm .
To prove. ABCD is a rhombus.
Proof. In || Sm, opposite sides are equal
∴ AB = CD
and AD = BC ……. (i)

By adding these tangents,
(AP + PB) + (CR + DR) = AS + BQ + CQ + DS
⇒ AB + CD = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC
⇒ AB + AB = BC + BC ……[From (i)
⇒ 2AB = 2BC
⇒ AB = BC …….(ii)
From (i) and (ii), AB = BC = CD = DA
∴ || ^gm ABCD is a rhombus.
Or
(b)

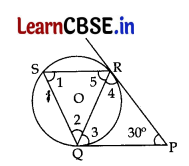
Given. ∠RPQ = 30°
To find the value of = ∠RQS
Proof: PQ = PR …[Tangents drawn from an external point are equal
∴ In ΔPQR, ∠3 = ∠4 …[Angles opposite to equal sides
∴ In ΔPQR, ∠3 + ∠4 + ∠30° = 180° …….(i)
…[Angles sum Property of a Δ
⇒ ∠3 + ∠3 + 30° = 180° …[From (i)
⇒ 2∠3 = 180° – 30° = 150°
⇒ ∠3 = \(\frac{150}{2}\) = 75°
∴ ∠3 = ∠4 = 75° ……(ii)
RS || PQ …[Given
∠5 = ∠3 = 75° …(iii) …[Alternate Interior angles
PQ is a tangent and QR is a chord.
∠1 = ∠3 = 75° …[Angles in the alternate segments
In ΔQRS, ∠1 + ∠2 + ∠5 = 180° …[Angles-sum-Property of a Δ
⇒ 75° + ∠2 + 75° = 180° …[From (ii) and (iii)
⇒ ∠2 = 180° – 75° – 75°
∴ ∠2 or ∠RQS = 30°