Students can use CBSE Previous Year Question Papers Class 10 Maths with Solutions and CBSE Class 10 Maths Question Paper 2022 (Term-II) to familiarize themselves with the exam format and marking scheme.
CBSE Class 10 Maths Question Paper 2022 (Term-II) with Solutions
Time allowed: 3 hours
Maximum marks: 80
General Instructions:
Read the following instructions carefully and follow them:
- This Question paper contains 14 Questions. All questions are compulsory.
- This Question Paper is divided into 3 Sections – Section A, B and C
- Section – A comprises of 6 questions (Q. Nos. 1 to 6) of 2 marks each. Internal choice has been provided in two questions.
- Section – B comprises of 4 questions (Q. Nos. 7 to 10) of 3 marks each. Internal choice has been provided in one questions.
- Section – C comprises of 4 questions (Q. Nos. 11 to 14) of 4 marks each. An internal choice has been provided in one question. It also contains two case study based questions.
- Use of calculator is not permitted.
- Question No. 6 and 10 have been replaced.
Section – A
Question numbers 1 to 6 carry 2 marks each.
Question 1.
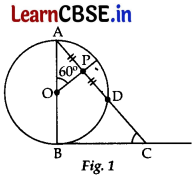
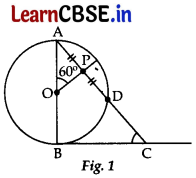
(a) In Figure 1, AB is diameter of a circle centered at O BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find m∠C.
Or
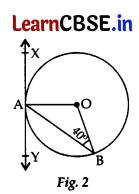
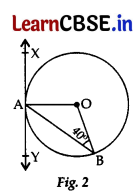
(b) In Figure 2, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find m∠BAY and m∠AOB.
Answer:
(a) AP = PD …[Given
OP⊥AD …[Perpendicular from centre bisect the chord
∴ ∠APO = 90°
In ΔAPO,
∠APO + ∠AOP + ∠OAP = 180° …[Angle-sum-property of a Δ
90° + 60° + ∠OAP = 180°
⇒ ∠OAP = 180° – 90° – 60° = 30° ….. (i)
…[Since BC in a tangent. (Given)
∴ ∠ABC = 90° …(ii)
…[Tangent is perpendicular to the radius through the point of contact
In ΔABC, ∠ABC + ∠BAC + m∠C = 180°
[Angle-sum-property of a Δ
90° + 30° + m∠C – 180° …[From (i) & (ii)
∴ m∠C = 180° – 90° – 30° = 60°
Or
(b) In ΔAOB, OA = OB …[Radii of the circle
∴ ∠OAB = ∠ABO
…[Angles opposite to equal sides are equal
∴ OAB = 40° ……(i)
Since OA is the radius and XAY is a tangent. …[Given
∴ ∠OAY = 90° …[Tangent in perpendicular to the radius through the point of contact
∠OAB + ∠BAY = 90°
⇒ 40° + ∠BAY = 90° …[From (i)
∴ ∠BAY = 90° – 40° = 50°
In ΔAOB,
∠OAB + ∠ABO + ∠AOB = 180°
…[Angle-sum-property of a Δ
40° + 40° + ∠AOB = 180°
∴ ∠AOB = 180° – 40° – 40° =100°
![]()
Question 2.
If mode of the following frequency distribution is 55, find the value of x.

Answer:
Mode = 55 (Given)
∴ Modal class is 45 – 60.
As we know,
Mode = l + \(\frac{f_1-f_0}{2 f_1-f_0-f_2}\) × h ∴ l = 45, f
0
= x, f
1
= 15, f
2
= 10, h = 15
⇒ 55 = 45 + \(\frac{15-x}{30-x-10}\) × 15
⇒ 55 – 45 = \(\frac{(15-x)}{20-x}\) × 15
⇒ 10(20 – x) = 225 – 15x
⇒ 200 – 10x = 225 – 15x
⇒ -10x + 15x = 225 – 200
⇒ 5x = 25 ∴ x = \(\frac{25}{5}\) = 5
Question 3.
(a) In an A.P. if the sum of third and seventh term is zero, find its 5
th
term.
Or
(b) Determine the A.P. whose third term is 5 and seventh term is 9.
Answer:
(a) Let a be the First term and d the common difference.
a
3
+ a
7
= 0 ….[Given
⇒ a + 2d + a + 6d = 0 ….[∵ a
n
= a + (n – 1)d
⇒ 2a + 8d = 0
⇒ 2 (a + 4d) = 0
⇒ a + 4d = 0
a
5
= 0 …[∵ a
5
= a + 4d
∴ 5
th
term = 0
Or
(b) Let a be the First term and d the common difference.
According to Question,
a
3
= 5
a + 2d = 5
a = 5 – 2d ……… (i)
a = 5 – 2(1) [From (ii)
∴ a = 5 – 2 = 3
a
7
= 9 [∵ a
n
= a + (n – 1)d
a + 6d = 9
5 – 2d + 6d = 9 [From (i)
4d = 9 – 5 = 4
∴ d = \(\frac{4}{4}\) = 1 …….. (ii)
∴ AP is a, a + d, a + 2d, ………….
3, 4, 5, 6, 7, …………….
Question 4.
Solve the quadratic equation: x
2
+ 2√2x – 6 = 0 for x.
Answer:
Given, x
2
+ 2√2x – 6 = 0
⇒ x
2
+ 3√2x – √2x – 6 = 0
⇒ x(x + 3√2) – √2(x + 3√2) = 0
⇒ (x – √2)(x + 3√2) = 0
x – √2 = 0 or x + 3√2 = 0
x = √2 or x = -3√2
Question 5.
Find the sum of first 20 terms of an A.P. whose n
th
term is given as a
n
= 5 – 2n.
Answer:
Given. a
n
= 5 – 2n
Put n = 1, a
1
= 5 – 2(1) = 3 = a
Put n = 2, a
2
= 5 – 2(2) = 1
∴ d = a
2
– a
1
= 1 – 3 = -2
Now, S
n
= \(\frac{n}{2}\)[2a + (n – 1)d]
∴ S
20
= \(\frac{20}{2}\)[2(3) + (20 – 1) (-2)]
= 10(6 – 38) = -320
Question 6.
A sphere of diameter 18 cm is dropped into a cylindrical vessel of diameter 36 cm, partly filled with water. If the sphere is completely submerged, then calculate the rise of water level (in c.m).
Answer:
Volume of Cylinder = Volume of Sphere
⇒ πR
2
h = \(\frac{4}{3}\) πr
3
⇒ (18)
2
h = \(\frac{4}{3}\) × (9)
3
…[∵ R = \(\frac{36}{2}\) = 18 cm; r = \(\frac{18}{2}\) = 9 cm
∴ h = \(\frac{4}{3}\) × \(\frac{9 \times 9 \times 9}{18 \times 18}\) = 3 cm
![]()
Section – B
Question numbers 7 to 10 carry 3 marks each.
Question 7.
(a) The mean of the following frequency distribution is 25. Find the value of.

Or
(b) Find the mean of the following data using assumed mean method:

Answer:
(a)
| Class | f i | x i | f i x i |
| 0 – 10 | 5 | 5 | 25 |
| 10 – 20 | 18 | 15 | 270 |
| 20 – 30 | 15 | 25 | 375 |
| 30 – 40 | f | 35 | 35f |
| 40 – 50 | 6 | 45 | 270 |
| Σf i = 44 + f | Σf i x i – 940 + 35f |
As we know, Mean = \(\frac{\sum f_i x_i}{\sum f_i}\)
\(\frac{25}{1}\) = \(\frac{940+35 f}{44+f}\)…[Mean = 25 (Given)
⇒ 940 + 35f = 25(44 + f)
⇒ 940 + 35f = 1100 + 25f
⇒ 35f – 25f = 1100 – 940
⇒ 10f= 160 ∴ f = \(\frac{160}{10}\) = 16
Or
(b)
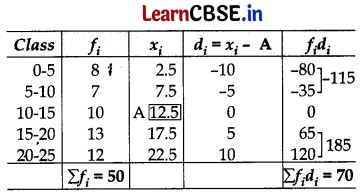
∴ Mean, \(\overline{\mathbf{X}}\) = A + \(\frac{\sum f_i d_i}{\sum f_i}\)
= 12.5 + (\(\frac{70}{50}\)) = 12.5 + 1.4 = 13.9
Question 8.
Find a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river
are 30° and 45°. If the bridge is at a height of 8.m from the banks, then the find the width of the river.
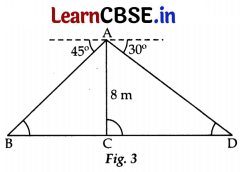
Answer:
Here, ∠ABC = 45° and ∠ADC = 30° …[Alternate Interior angles
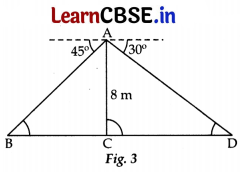
In right angle ΔACB,
tan 45° = \(\frac{\mathrm{AC}}{\mathrm{BC}}\)
⇒ 1 = \(\frac{8}{B C}\) BC ∴ BC = 8 m ……. (i)
In right angle ΔACD,
tan 30° = \(\frac{\mathrm{AC}}{\mathrm{CD}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{8}{\mathrm{CD}}\)
∴ CD = 8√3 m ……… (ii)
Now, Width of the river, BD = BC + CD
= 8 + 8√3 …[From (i) and (ii)
= 8(1 + √3)m
= 8(1 + 1.73) …[∵ √3 = 1.73
= 21.84 m
Question 9.
Heights of 50 students of class X of a school are recorded and following data is obtained:

Find the median height of the students.
Answer:
| Height (in cm) | f i | c.f. |
| 130 – 135 | 4 | 4 |
| 135 – 140 | 11 | 15 c.f. |
| 140 – 145 | 12f | 27 |
| 145 – 150 | 7 | 34 |
| 150 – 155 | 10 | 44 |
| 155 – 160 | 6 | 50 |
| Σf i = 50 |
Here, \(\frac{n}{2}\) = \(\frac{50}{2}\) = 25
Median class is 140 – 145.
∴ l = 140, f = 12, c.f. = 15, h = 5
As we know, Median = l + \(\frac{\frac{n}{2}-c . f .}{f}\) × h
= 140 + \(\frac{(25-15)}{12}\) × 5
= 140 + \(\frac{50}{12}\) = 140 + 4.1\(\overline{6}\) = 144.1\(\overline{6}\) cm
Question 10.
Through the mid-point, M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC at L and AD produced to E. Prove that EL. 2BL.
Answer:
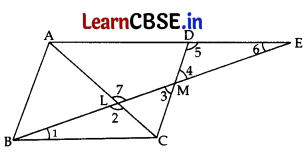
Given. In a ||gm ABCD, M is the midpoint of CD.
To Prove: EL = 2 BL
Proof: In ΔBMC and ΔEMD,
∠3 = ∠4 …[Vertically opposite angles
MC = MD …[M is the mid-point of CD
∠BCM = ∠5 …[Alternate interior angles
∴ ΔBMC ☐ ΔEMD …[ASA congruence rule
∴ BC = DE (i)..[CPCT
BC = AD (ii)…[Opposite sides of || gm
BC + BC = DE + AD …[Adding (i) & (ii)
2BC = AE …(iii)
In ΔALE and ΔCLB,
∠7 = ∠2 …[Vertically opposite angles
∠6 = ∠1 …[Alternate interior angles
ΔALE ~ ΔCLB ..[AA similarity criterion
\(\frac{\mathrm{AE}}{\mathrm{CB}}=\frac{\mathrm{LE}}{\mathrm{BL}}\) …ICPST
⇒ \(\frac{2 B C}{C B}=\frac{E L}{B L}\) …[From (iii)
∴ EL = 2BL (Hence Proved)
![]()
Section – C
Question numbers 11 to 14 carry 4 marks each.
Question 11.
(a) A 2-digit number is such that the product of its digits is 24. If 18 is subtracted from the number, the digits interchange their places. Find the number.
Or
(b) The difference of the squares of two numbers is 180. The square of the smaller number is 8 times the greater number. Find the two numbers.
Answer:
(a) Let the ten’s place digit be x and then the unit’s place digit be \(\frac{24}{x}\).
∴ Original number = 10x + \(\frac{24}{x}\)
Interchanged number = 1 × x + 10(\(\frac{24}{x}\)) = x + \(\frac{240}{x}\)
According to Question,
10x + \(\frac{24}{x}\) – 18 = x + \(\frac{240}{x}\)
⇒ 10x + \(\frac{24}{x}\) – 18 – x – \(\frac{240}{x}\) = 0
⇒ \(\frac{10 x^2+24-18 x-x^2-240}{x}\) = 0
⇒ 9x
2
– 18x – 216 = 0
⇒ x
2
– 2x – 24 = 0 …[Dividing both sides by 9
⇒ x
2
– 6x + 4x – 24 = 0
⇒ x(x – 6) + 4 (x – 6) = 0
⇒ (x – 6) (x + 4) = 0
⇒ x – 6 = 0 or x + 4 = 0
∴ x = 6 or x = -4 …[Not possible as Digit cannot be negative.
∴ Original number = 10(6) + \(\frac{1}{2}\) = 60 + 4 = 64
Or
(b) Let the Greater number be x
and the smaller number be y.
According to Question,
x
2
– y
2
= 180
(Smaller number)
2
= 8(Greater number) and y
2
= 8x …..(i)
⇒ x
2
– 8x – 180 = 0 …[From (i)
⇒ x
2
– 18x + 10x – 180 = 0
⇒ x(x – 18) + 10 (x – 18) = 0
⇒ (x – 18) (x + 10) = 0
⇒ x – 18 = 0 or x + 10 = 0
⇒ x = 18 or x = -10
When x = 18
from (i), y
2
= 8x
y
2
= 8(18)
y
2
= 144
∴ y ± 12
When x = -10
from (i), y
2
= 8x
y
2
= -80 (rejected as
y
2
can not be -ve)
∴ Numbers are 18,12 or 18, -12.
Question 12.
Prove that a parallelogram circumscribing a circle is a rhombus.
Answer:
Given: ABCD is 11 gm.
To Prove:ABCD is a rhombus.
Proof: In || gm, opposite sides are equal.
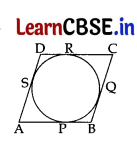
AB = CD and AD = BC …(i)

By adding (ii), (iii), (iv) and (v), we get
AP + BP + CR + DR = AS + BQ + CQ + DS (AP + BP) + (CR + DR) = (BQ + CQ) + (AS + DS)
AB + CD = BC + AD
AB + AB = BC + BC …..[From (i)
2AB = 2BC
∴ AB = BC …..(vi)
From (i) and (vi), AB = BC = CD = DA
∴ ABCD is a rhombus.
Question 13.
Case Study – 1:
Kite Festivel
Kite festival is celebrated in many countries at different times of the year. In india, every year 14
th
January is celebrated as International Kite Day. On this day many people visit India and participate in the festival by flying various kinds of kites.
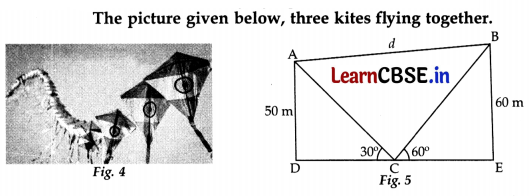
In figure 5, the angles of elevation of two kites (Points A and B) from the hands of a man (Point C) are found to be 30° and 60° respectively. Taking AD = 50 m and BE = 60 m, find
(a) the lengths of strings used (take them straight) for kites A and B as shown in the figure. 2
(b) the distance ‘d’ between these two kites. 2
Answer:
Since DCE is a straight line.
∠ACD + ∠ACB + ∠BCE = 180° …[Linear pair
⇒ 30° + ∠ACB + 60° = 180°
⇒ ∠ACB = 180° – 30° – 60°
∴ ∠ACB = 90° …(i)
(a) In right angle ΔADC,
sin30° = \(\frac{\mathrm{AD}}{\mathrm{AC}}\)
⇒ \(\frac{1}{2}\) = \(\frac{50}{\mathrm{AC}}\)
∴ AC = 100 m ……(ii)
In right angle ΔBEC,
sin 60° = \(\frac{\mathrm{BE}}{\mathrm{BC}}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{60}{B C}\) ⇒ √3 BC = 120
∴ BC = \(\frac{120}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{120 \sqrt{3}}{3}\)
= 40√3 m ……(iii)
∴ Length of strings are 100 m and 40√3
(b) From (i), In right angle ΔACB,
AB
2
= AC
2
+ BC
2
…[Using pythagoras’ theorem
d
2
= (100)
2
+ (40√3)
2
…[From (ii) and (iii)
⇒ d
2
= 10,000 + 4,800
⇒ d
2
= 14,800
⇒ d = \(\sqrt{14,800}\) or 121.655
∴ d (distance between two kites) = 121.7 m approx.
![]()
Question 14.
Case Study – 2:
A ‘circus’ is a company of performers who put on shows of acrobats, clowns etc. to entertain people started around 250 years back, in open fields, now generally performed in tents. One such ‘Circus Tent’ is shown below.

The tent is in the shape of cylinder surmounted by a conical top. If the height and diameter of cylindrical part are 9 m and 30 m respectively and height of conical part is 8 m with same diameter as that of cylindrical part, then find
(a) the area of the canvas used in making the tent; 3
(b) the cost of the canvas bought for the tent at the rate ?200 per sq. m, if 30 sq. m canvas was wasted during stitching. 1
Answer:
(a) Let height of cone, h
1
= 8 m and height of cylinder, h
2
= 9 m
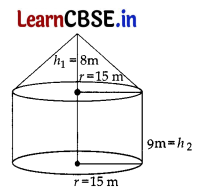
Radius, r = \(\frac{30}{2}\) = 15 m
Here, Slant height, l = \(\sqrt{r^2+h_1^2}\)
⇒ l = \(\sqrt{15^2+8^2}\)
⇒ l = \(\sqrt{225+64}\)
⇒ l = \(\sqrt{289}\)
∴ l = 17 m
Now, Area of canvas used in making the tent = Area of cylinder + Area of cone
= 2πrh
2
+ πrl
= πr(2h
2
+ l)
= \(\frac{22}{7}\) × 15[2(9) + 17]
= \(\frac{22}{7}\) × 15 × 35 = 1650 m
2
(b) Actually canvas used after wastage.
= 1650 + 30 = 1680 m
2
∴ Cost of canvas @ ₹200 per square meter
= 1680 m
2
× ₹200 = ₹3,36,000