CBSE Class 10 Maths Question Paper 2021 (Term-I) with Solutions

Students can use CBSE Previous Year Question Papers Class 10 Maths with Solutions and CBSE Class 10 Maths Question Paper 2021 (Term-I) to familiarize themselves with the exam format and marking scheme.

CBSE Class 10 Maths Question Paper 2021 (Term-I) with Solutions

Time allowed: 3 hours
Maximum marks: 80

General Instructions:
Read the following instructions carefully and follow them:

1. This Question paper contains 50 questions out of which 40 questions are to be attempted as per instructions. All questions carry equal marks
2. This Question paper consists three Sections – Section A, B and C.
3. Section – A contains 20 questions. Attempt any 16 questions from Q. No. 1 to 20.
4. Section – B also contains 20 questions. Attempt any 16 questions from Q. No. 21 to 40.
5. Section – C contains of two Case Studies containing 5 questions in each case. Attempt any 4 questions from Question No. 41 to 45 and another 4 from Question No. 46 to 50.
6. There is only one correct option for every Multiple Choice Question (MCQ). Marks will not be awarded for answering more than one option.
7. There is no negative marking.

Section – A

Q.No. 1 to 20 are of 1 mark each. Attempt any 16 from Q. 1 to 20.

Question 1.
The exponent of 5 in the prime factorisation of 3750 is
(a) 3
(b) 4
(c) 5
(d) 6
Answer:
(b) 4
3750 = 2 × 3 × 5 ⁴

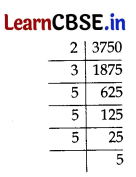
∴ Exponent of 5 is 4.

Question 2.
The graph of a polynomial P(x) cuts the x-axis at 3 points and touches it at 2 other points. The number of zeroes of P(x) is
(a) 1
(b) 2
(c) 3
(d) 5
Answer:
(d) 5
P(x) cuts the x-axis at 3 points and tocuhes it at 2 other points.
∴ The number of zeroes of P(x) is (3 + 2) = 5

Question 3.
The values of x and y satisfying: the two equations 32x + 33y = 34, 33x + 32y = 31 respectively are:
(a) -1, 2
(b) -1, 4
(c) 1, -2
(d) -1, -4
Answer:
(a) -1, 2

Putting y = 2 in (iii), we get
x + 2 = 1 ⇒ x = -1
∴ x = -1 and y = 2

Question 4.
If A (3, √3 ), B(0, 0) and C(3, k) are the three vertices o$ an equilateral triangle ABC, then the value of k is
(a) 2
(b) -3
(c) -√3
(d) -√2
Answer:
(c) -√3
In ΔABC, AB = BC
…[All sides of an equilateral Δ is equal
AB ² = BC …[squaring both sides
(0 – 3) ² + (o – √3) ² = (3 – 0) ² + (k – 0) ²
⇒ 9 + 3 = 9 + k ² ⇒ k = ±√3
But only k = -√3 has been given in the option.

Question 5.
In figure, DE || BC, AD = 2 cm and BD = 3 cm and AC = 7.5 cm then EC is equal to

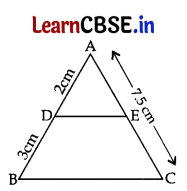
(a) 3 cm
(b) 3.5 cm
(c) 4 cm
(d) 4.5 cm
Answer:
(d) 4.5 cm
In ΔABC, DE||BC …[Given

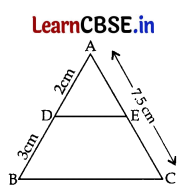
\(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\) …[Thales’ theorem
⇒ \(\frac{2}{3}\) = \(\frac{7.5-x}{x}\) ….[Let EC = x cm then AE = (7.5 – x) cm
⇒ 2x = 22.5 – 3x
⇒ 5x = 22.5
⇒ x = \(\frac{22.5}{5}\) = 4.5 cm
∴ EC = x = 4.5 cm

Question 6.
If cot θ = \(\frac{1}{\sqrt{3}}\), the value of sec ² θ + cosec ² θ is
(a) 1
(b) \(\frac{40}{9}\)
(c) \(\frac{38}{9}\)
(d) 5\(\frac{1}{3}\)
Answer:
(d) 5\(\frac{1}{3}\)
Given, cot θ = \(\frac{1}{\sqrt{3}}\)
⇒ cot θ = cot 60°
∴ θ = 60°
Now, sec ² θ + cosec ² θ
= sec ² 60° + cosec ² 60° [∵ θ = 60°
= (2) ² + (\(\frac{2}{\sqrt{3}}\)) ²
4 + \(\frac{4}{3}\) = \(\frac{12+4}{3}\)
= \(\frac{16}{\sqrt{3}}\) or 5\(\frac{1}{\sqrt{3}}\)

Question 7.
The area of a quadrant of a circle where the circumference of circle is 176 m, is
(a) 2464 m ²
(b) 1232 m ²
(c) 616 m ²
(d) 308 m ²
Answer:
(c) 616 m ²
Given. Circumference of circle = 176 m
⇒ 2πr = 176
⇒ 2 × \(\frac{22}{7}\) × r = 176
⇒ r = \(\frac{176 \times 7}{2 \times 22}\) = 28 m
∴ Area of Quadrant of a circle = – \(\frac{1}{4}\)πr ²
= \(\frac{1}{4}\) × \(\frac{22}{7}\) × 28 × 28 = 616 m ²

Question 8.
For an event E, P(E) + P (\(\overline{\mathbf{E}}\)) = x, then the value of x ³ – 3 is
(a) -2
(b) 2
(c) 1
(d) -1
Answer:
(a) -2
As we know, P(E) + P( \(\overline{\mathbf{E}}\)) = 1
Also, P(E) + P(\(\overline{\mathbf{E}}\)) = x …[Given
∴ x = 1
Now, (x) ³ – 3 = 1 ³ – 3 = 1 – 3 = -2

Question 9.
What is the greatest possible speed at which a girl can walk 95 m and 171 m in an exact number of minutes?
(a) 17 m/min.
(b) 19 m/min.
(c) 23 m/min.
(d) 13 m/min.
Answer:
(b) 19 m/min.
95 = 5 × 19
171 = 3 ² × 19
∴ HCF (95,191) = 19 m/min.

Question 10.
In figure, the graph of a polynomial P(x) is shown. The number of zeroes of P(x) is

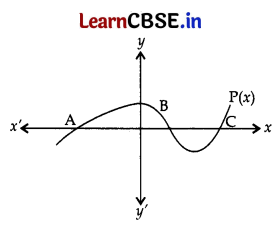
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(c) 3
The number of zeroes is 3 as the graph intersects the x-axis at 3 points i.e., A, B and C.

Question 11.
Two lines are given to be parallel. The equation of one of the lines is 3x – 2y = 5. The equation of the second line can be
(a) 9x + 8y = 7
(b) -12x – 8y = 7
(c) -12x + 8y = 7
(d) 12x + 8y = 7
Answer:
(c) -12x + 8y = 7
When Lines are parallel:
\(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
Given. 3x – 2y = 5
Check at option (c), -12x + 8y = 7
Here,
\(\frac{a_1}{a_2}\) = \(\frac{3}{-12}\) = –\(\frac{1}{4}\); \(\frac{b_1}{b_2}\) = \(\frac{-2}{8}\) = \(\frac{-1}{4}\); \(\frac{c_1}{c_2}\) = \(\frac{5}{7}\)
∴ \(\frac{-1}{4}\) = \(\frac{-1}{4}\) ≠ \(\frac{5}{7}\)

Question 12.
Three vertices of a parallelogram ABCD are A(1, 4), B(-2, 3) and C(5, 8). The ordinate of the fourth vertex D is
(a) 8
(b) 9
(c) 7
(d) 6
Answer:
(b) 9
Let D(a, b) be the 4 ^th vertex.

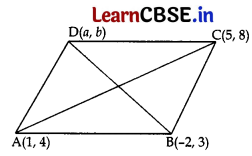
In || gm, Diagonals bisect each other.
∴ Mid-point of AC = Mid-point of BD
(\(\frac{1+5}{2}, \frac{4+8}{2}\)) (\(\frac{a-2}{2}, \frac{b+3}{2}\))
For ordinate, \(\frac{12}{2}\) + \(\frac{b+3}{2}\)
∴ b = 12 – 3 = 9

Question 13.
In ΔABC and ΔDEF, ∠F = ∠C, ∠B = ∠E and AB = \(\frac{1}{2}\) DE. Then, the two triangles are
(a) Congruent, but not similar.
(b) Similar, but not congruent.
(c) Neither congruent nor similar.
(d) Congruent as well as similar.
Answer:
(b) Similar, but not congruent.
For triangles congruency,
There are five rules for congruency (i) SAS; (ii) ASA; (iii) AAS; (iv) SSS; (v) RHS

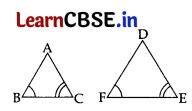
If in two triangles, two angles of one triangle are respectively equal to the two angles of the other triangle, then the two trinagles are similar (AA similarity criterion)
Since there is not any congrency criteria like AA.
∴ Given triangles similar, but not congruent.

Question 14.
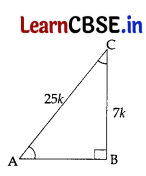
In ΔABC right angled at B, sin A = \(\frac{7}{25}\), then the value of cos C is
(a) \(\frac{7}{25}\)
(b) \(\frac{24}{25}\)
(c) \(\frac{7}{24}\)
(d) \(\frac{24}{7}\)
Answer:
(a) \(\frac{7}{25}\)
(a) Given, sin A = \(\frac{7}{25}\)
Let BC = 7k and AC = 25k
∴ cos C = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7 k}{25 k}\)
∴ cos C = \(\frac{7}{25}\)

Question 15.
The minute hand of a clock is 84 cm long. The distance covered by the tip of minute hand from 10 :10 am to 10 : 25 am is
(a) 44 cm
(b) 88 cm
(c) 132 cm
(d) 176 cm
Answer:
(c) 132 cm
(c) Time = 10 : 25 – 10 : 10 = 15 mins Angle described by minute hand in one minute = \(\frac{360^{\circ}}{60}\) = 6°
∴ Angle described by minute hand in 15 minutes = (15 × 6)° = 90°
∴ Distance covered by the tip of minute hand in 15 minutes
= \(\frac{\theta}{180^{\circ}}\)(πr) = \(\frac{90^{\circ}}{180^{\circ}}\) × \(\frac{22}{7}\) × 84 = 132 cm [∵ r = 84 cm (given)

Question 16.
The probability that the drawn card from a pack of 52 cards is neither an ace nor a spade is
(a) \(\frac{9}{13}\)
(b) \(\frac{35}{52}\)
(c) \(\frac{10}{13}\)
(d) \(\frac{19}{26}\)
Answer:
(a) \(\frac{9}{13}\)
P(neither an ace nor a spade)
= 1 – P(Ace or spade)
= 1 – (P(Ace) + P(spade) – P(Ace and spade))
= 1 – (\(\frac{4}{52}\) + \(\frac{13}{52}\) – \(\frac{1}{52}\))
= 1 – \(\frac{16}{52}\) = \(\frac{36}{52}\) = \(\frac{9}{13}\)

Question 17.
Three alarm clocks ring their alarms at regular intervals of 20 min, 25 min and 30 min respectively. If they first beep together at 12 noon, at what time will they beep again for the first time?
(a) 4 : 00 pm
(b) 4 : 30 pm
(c) 5 : 00 pm
(d) 5 : 30 pm
Answer:
(c) 5 : 00 pm
First alarm time = 20 mins = 2 ² × 5
Second alarm time = 25 mins = 5 ²
Third alarm time = 30 mins = 2 × 3 × 5
LCM of (20, 25, 30) = 2 ² × 3 × 5 ²
= 300 minutes = \(\frac{300}{60}\) = 5 hours
∴ They will beep again after 5 hours = 12 noon + 5 hrs = 5 : 00 pm

Question 18.
A quadratic polynomial, the product and sum of whose zeroes are 5 and 8 respectively is
(a) k[x ² – 8x + 5]
(b) k[x ² + 8x + 5]
(c) k[x ² – 5x + 8]
(d) k[x ² + 5x + 8]
Answer:
(a) k[x ² – 8x + 5]
Quadratic polynomial is
A:(x ² – (sum of zeroes)x + product of zeroes), where k is non-zero real number.
= k[x ² – 8x + 5]

Question 19.
Points A (-1, y) and B(5, 7) lie on a circle with centre O (2, -3y). The values of y are
(a) 1, -7
(b) -1, 7
(c) 2, 7
(d) -2, -7
Answer:
(b) -1, 7
OA – OB …[Radii of circle
OA ² = OB ² …[squaring both sides

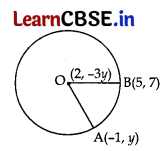
(-1 – 2) ² + (y + 3y) ² = (5 – 2) ² + (7 + 3y) ²
⇒ 9 + (4y) ² = 9 + 49 + 9y ² + 42 y
⇒ 16y ² – 9y ² – 42y – 49 = 0
⇒ 7y ² – 42y – 49 = 0
⇒ y ² – 6y – 7 = 0
⇒ y ² – 7y + y – 7 = 0
⇒ y(y – 7) + 1(y – 7) = 0
⇒ (y – 7)(y + 1) = 0
⇒ y – 7 = 0 or y + 1 = 0
∴ y = 7 and -1

Question 20.
Given that sec θ = √2 , the value of \(\frac{1+\tan \theta}{\sin \theta}\) is
(a) 2√2
(b) √2
(c) 3√2
(d) 2
Answer:
(a) 2√2
(a) Given, sec θ = √2
sec θ = sec 45°
⇒ θ = 45°
Now, \(\frac{1+\tan \theta}{\sin \theta}=\frac{1+\tan 45^{\circ}}{\sin 45^{\circ}}\)
= \(\frac{1+1}{\frac{1}{\sqrt{2}}}\) = 2 \(\frac{\sqrt{2}}{1}\) = √2

Section – B

Q. No. 21 to 40 are of 1 mark each. Attempt any 16 from Q. 21 to 40.

Question 21.
The greatest number which when divides 1251, 9377 and 15628 leaves remainder 1, 2 and 3 respectively is
(a) 575
(b) 450
(c) 750
(d) 625
Answer:
(d) 625
The required number is the HCF of the numbers

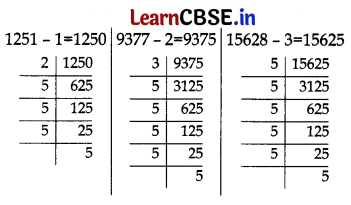
Here, 1250 = 2 × 5 ⁴
9375 = 3 × 5 ⁵
15625 = 5 ⁶
∴ HCF (1250, 9375,15625) = 5 ⁴ = 625

Question 22.
Which of the following cannot be the probability of an event?
(a) 0.01
(b) 3%
(c) \(\frac{16}{17}\)
(d) \(\frac{17}{16}\)
Answer:
(d) \(\frac{17}{16}\)
The probability of an event E is a number P(E) such that 0 ≤ P(E) ≤ 1 So, Probability of an event cannot be more than 1.
∴ P(an event) = \(\frac{17}{16}\) = 1 \(\frac{1}{16}\) cannot possible.

Question 23.
The diameter of a car wheel is 42 cm. The number of complete revolutions it will make in moving 132 km is
(a) 10 ⁴
(b) 10 ⁵
(c) 10 ⁶
(d) 10 ³
Answer:
(b) 10 ⁵
Radius, r = \(\frac{42}{2}\) = 21 cm
Distance covered by wheel in one revolution = 2πr
= 2 × \(\frac{22}{7}\) × 21 = 132 cm
Here, 1km = 1000 m, 1m = 100 cm
132 km = 132 × 100 × 1000 cm
∴ Number of complete revolutions
= \(\frac{\text { Total distance }}{2 \pi r}\)
= \(\frac{132 \times 100 \times 1000}{132}\) = 10 ⁵

Question 24.
If θ is an acute angle and tan θ + cot θ = 2, then the value of sin ³ θ + cos ³ θ is
(a) 1
(b) \(\frac{1}{2}\)
(c) \(\frac{\sqrt{2}}{2}\)
(d) √2
Answer:
(c) \(\frac{\sqrt{2}}{2}\)
We have, tan θ + cot θ = 2
tan θ + \(\frac{1}{\tan \theta}\) = 2
⇒ \(\frac{\tan ^2 \theta+1}{\tan \theta}\) = 2
⇒ tan ² θ + 1 = 2 tan θ
⇒ tan ² θ – 2 tan θ + 1 = 0
⇒ (tan θ – 1) ² = 0 …[∵ a ² – 2ab + b ² = (a – b) ²
⇒ tan θ – 1 = 0 => tan θ = 1
⇒ tan θ = tan 45°
∴ θ = 45°

Question 25.
The ratio in which the line 3x + y – 9 = 0 divides the line segment joining the points (1, 3) and (2, 7) is
(a) 3 : 2
(b) 2 : 3
(c) 3 : 4
(d) 4 : 3
Answer:
(c) 3 : 4

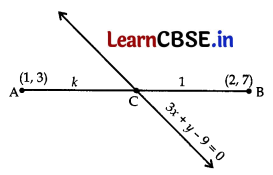
Let AC : CB = k : 1
∴ Coordinate C = (\(\frac{2 k+1}{k+1}, \frac{7 k+3}{k+1}\)) …[using section formulae
Since Point C lies in the given line 3x + y – 9 = 0
3\(\left(\frac{2 k+1}{k+1}\right)+\frac{7 k+3}{k+1}\) – 9 = 0
\(\frac{6 k+3+7 k+3-9 k-9}{k+1}\) = 0
4k – 3 = 0 ⇒ k = \(\frac{3}{4}\)
∴ Required Ratio = k : 1 = \(\frac{3}{4}\) : 1 = 3 : 4

Question 26.
If x – 1 is a factor of the polynomial P(x) = x ³ + ax ² + 2b and a + b = 4, then
(a) a = 5,b = -1
(b) a = 9, b = -5
(c) a = 7, b = -3
(d) a = 3, b = 1
Answer:
(b) a = 9, b = -5
p(x) = x ³ + ax + 2b
Since (x – 1) is a factor of p(x).
∴ P(1) = 0
(1) ³ + a(1) + 2b = 0
a = – 2b – 1 …(i)
a + b = 4 or a = 4 – b ……(ii)
Solving (i) and (ii) – 2b – 1 = 4 – b
– b = 5 ⇒ b = -5
From (ii), a – 5 = 4
⇒ a = 9
∴ a = 9, b = -5

Question 27.
If a and b are two coprime numbers, then a ³ and b ³ are
(a) Co-prime
(b) Not co-prime
(c) Even
(d) Odd
Answer:
(a) Co-prime
As we know, If a and b are two coprime numbers then a ³ and b ³ are also coprime.
For Example, Let a = 2, b = 3,
∴ HCF(2, 3) = 1
a ³ = 2 ³ = 8; b ³ = (3) ³ = 27, HCF(8, 27) = 1
Therefore, 8 and 27 are coprime numbers.

Question 28.
The area of a square that can be inscribed in a circle of area \(\frac{1408}{7}\) cm ² is
(a) 321 cm ²
(b) 642 cm ²
(c) 128 cm ²
(d) 256 cm ²
Answer:
(c) 128 cm ²
Area of circle = \(\frac{1408}{7}\)cm ² ..[Given

⇒ πr ² = \(\frac{1408}{7}\) ⇒ \(\frac{22}{7}\) r ² = \(\frac{1408}{7}\)
⇒ r ² = \(\frac{1408}{22}\) = 64
∴ r = 8 cm …[∵ Radius can not be negative Diagonal of Square = AC = 2r
= 2(8) = 16 cm
Now, Area of a Square
= \(\frac{1}{2}\)(diagonal) ²
= \(\frac{1}{2}\) × 16 × 16 = 128 cm ²

Question 29.
If A (4, -2), B(7, -2) and C(7, 9) are the vertices of a ΔABC, then ΔABC is
(a) equilateral triangle
(b) isosceles triangle
(c) right-angled triangle
(d) isosceles right-angled triangle
Answer:
(c) right-angled triangle
AB = \(\sqrt{(7-4)^2+(-2+2)^2}\) = √9 = 3
BC = \(\sqrt{(7-7)^2+(9+2)^2}\) = \(\sqrt{11^2}\) = 11
AC = \(\sqrt{(7-4)^2+(9+2)^2}\) = \(\sqrt{9+121}\)
= \(\sqrt{130}\)
Here, AC ² = 130
and AB ² + BC ² = (3) ² + (11) ²
= 9 + 121 = 130 = AC ²
∴ ΔABC is right angled triangle.

Question 30.
If α, β are the zeroes of the quadratic polynomial p(x) = x ² – (k + 6)x + 2(2k – 1), then the value of k, if α + β = \(\frac{1}{2}\) αβ, is
(a) -7
(b) 7
(c) -3
(d) 3
Answer:
(b) 7
Here a = 1, b = -(k + 6), c = 2(2k – 1)
Sum of zeroes, α + β = \(\frac{-b}{a}\)
∴ α + β = \(\frac{(k+6)}{1}\) = k + 6
Product of zeroes, αβ = \(\frac{c}{a}\) = 2(2k – 1)
Now, α + β = \(\frac{1}{2}\)αβ …[Given
⇒ k + 6 = \(\frac{1}{2}\) × 2(2k – 1)
⇒ k + 6 = 2k – 1
⇒ 6 + 1 = 2k – k ∴ k = 7

Question 31.
If n is a natural number, then 2(5 ⁿ + 6 ⁿ ) always ends with
(a) 1
(b) 4
(c) 3
(d) 2
Answer:
(d) 2
Natural nos. are 1, 2, 3, 4, 5, ……..
Given. 2(5 ⁿ + 6 ⁿ )
when n = 1, 2(5 ¹ + 6 ¹ ) = 2(11) = 22
when n = 2, 2(5 ² + 6 ² ) = 2(25 + 36) = 2(61) = 132
when n = 3, 2(5 ³ + 6 ³ ) = 2(125 + 216) = 2(341) = 682
Therefore, 2(5 ⁿ + 6 ⁿ ) ends with digit 2.

Question 32.
The line segment joining the points P(-3, 2) and Q(5, 7) is divided by the y-axis in the ratio
(a) 3 : 1
(b) 3 : 4
(c) 3 : 2
(d) 3 : 5
Answer:
(d) 3 : 5

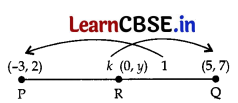
Let PR : RQ = k : 1
Coordinate R = \(\left(\frac{5 k-3}{k+1}, \frac{7 k+2}{k+1}\right)\) …[Using Section formula
Let point R(0, y) lies on y-axis.
∴ \(\frac{5 k-3}{k+1}\) = 0
⇒ 5k – 3 = 0 ⇒ k = \(\frac{3}{5}\)
∴ Required ratio = k : 1 = \(\frac{3}{5}\) : 1 = 3 : 5

Question 33.
If a cot θ + b cosec θ = p and b cot θ + a cosec θ = q, then p ² – q ² =
(a) a ² – b ²
(b) b ² – a ²
(c) a ² + b ²
(d) b – a
Answer:
(b) b ² – a ²
We have, p ² – q ²
= (a cot θ + b cosec θ) ² – (b cot θ + a cosec θ) ²
= a ² cot ² θ + b ² cosec ² θ + 2ab cot θ cosec θ – b ² cot ² θ – a ² cosec ² θ – 2ab cot θ cosec θ
= b ² (cosec ² θ – cot ² θ) – a ² (cosec ² θ – cot ² θ)
= b ² – a ² …[∵ cosec ² θ – cot ² θ = 1

Question 34.
If the perimeter of a circle is half to that of a square, then the ratio of the area of the circle to the area of the square is
(a) 22 : 7
(b) 11 : 7
(c) 7 : 11
(d) 7 : 22
Answer:
(d) 7 : 22
Let side of square be x units.
Perimeter (Circle) = \(\frac{1}{2}\) Perimeter (Square) (Given)
⇒ 2πr = \(\frac{1}{2}\)(4x)
⇒ πr = x ….. (i)
Now, \(\frac{\text { Area of Circle }}{\text { Area of Square }}=\frac{\pi r^2}{x^2}\)
= \(\frac{\pi r^2}{\pi^2 r^2}\) ….From (i)
= \(\frac{1}{\pi}\) = \(\frac{7}{22}\) = 7 : 22

Question 35.
A dice is rolled twice. The probability that 5 will not come up either time is
(a) \(\frac{11}{36}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{13}{36}\)
(d) \(\frac{25}{36}\)
Answer:
(d) \(\frac{25}{36}\)
Since a dice in rolled twice
∴ Total numbers of ways = 6 × 6 = 36
∴ P(5 will not come up)
= 1 – P(5 will come at least once)
= 1 – \(\frac{11}{36}\) [(5, 1)(5, 2)(5, 3)(5, 4)(5, 5) (5, 6)(1, 5)(2, 5)(3, 5) (4, 5)(6, 5)i.e., 11ways]
= \(\frac{25}{36}\)

Question 36.
The LCM of two numbers is 2400. Which of the following CANNOT be their HCF?
(a) 300
(b) 400
(c) 500
(d) 600
Answer:
(c) 500
As HCF is always be a factor of LCM but here 500 is not a factor of 2400. \(\frac{2400}{500}\) = \(\frac{24}{5}\) = 4.8

Question 37.
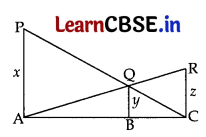
In figure, PA, QB and RC are each perpendicular to AC. If x = 8 cm and z = 6 cm, then y is equal to

(a) \(\frac{56}{7}\) cm
(b) \(\frac{7}{56}\) cm
(c) \(\frac{25}{7}\) cm
(d) \(\frac{24}{7}\) cm
Answer:
(d) \(\frac{24}{7}\) cm
Given. PA⊥AC, QB⊥AC and RC⊥AC
⇒ PA || QB || RC
⇒ ΔBQC ~ ΔAPC
⇒ \(\frac{\mathrm{BQ}}{\mathrm{PA}}\) = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
⇒ \(\frac{y}{x}\) = \(\frac{\mathrm{BC}}{\mathrm{AC}}\) ….. (i)
ΔABQ ~ ΔACR…[AA similarity
\(\frac{\mathrm{QB}}{\mathrm{AC}}\) = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
\(\frac{y}{z}\) = \(\frac{\mathrm{AB}}{\mathrm{AC}}\) …. (ii)
Adding (i) and (ii)

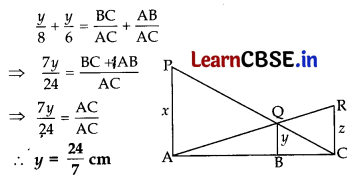
Question 38.
In a ΔABC, ∠A = x°, ∠B = (3x – 2)° ∠C = y°. Also ∠C – ∠B = 9°. The sum of the greatest and the smallest angles of this triangle is
(a) 107°
(b) 135°
(c) 155°
(d) 145°
Answer:
(a) 107°
Given. ∠A = x°; ∠B = (3x – 2)°; ∠C = y°
∠C = ∠B = 9° …..[Given
y – (3x – 2)° = 9°
y = 9 + 3x – 2° …(i)
In ΔABC,
x + (3x – 2 ) + y = 180° …[Angle-sum-property of a Δ
4x – 2 + 9 + 3x – 2 = 180° …[From (i)
7x = 180° + 4 – 9
7x = 175° ⇒ x = \(\frac{175^{\circ}}{7}\) = 25°
Now, ∠A = x° = 25° …[smallest
∠B = 3(25) – 2 = 73°
∠C = 180° – ∠A – ∠B = 82° …[greatest
∴ Sum of greatest and smallest angle
= 82° + 25° = 107°

Question 39.
If sec θ + tan θ = p, then tan θ is
(a) \(\frac{p^2+1}{2 p}\)
(b) \(\frac{p^2-1}{2 p}\)
(c) \(\frac{p^2-1}{p^2+1}\)
(d) \(\frac{p^2+1}{p^2-1}\)
Answer:
(b) \(\frac{p^2-1}{2 p}\)
As we know, sec ² θ – tan ² θ = 1
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1 …[a ² – b ² = (a + b) (a – b)
⇒ p(sec θ – tan θ) = 1 …[sec θ + tan θ = p (given)

Question 40.
The base BC of an equilateral AABC lies on the i/-axis. The co-ordinates of C are (0, -3).
If the origin is the mid-point of the base BC, what are the co-ordinates of A and B?
(a) A(√3, 0), B(0, 3)
(b) A(±3√3, 0), B(3, 0)
(c) A(±3√3, 0), B (0, 3)
(d) A (-√3, 0), B (3, 0)
Answer:
(b) A(±3√3, 0), B(3, 0)
C(0, -3) ….Given
∴ OC = 3units
and OB = 3 units …(∵ O is the mid-point of BC
∴ BC = 3 + 3 = 6units
AB = AC = 6 …[All sides of an equilateral Δ are equal

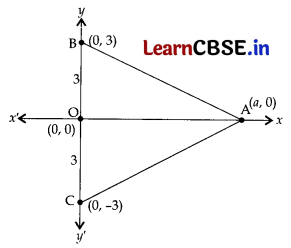
Let A(a, 0) be point on x-axis.
∴ AB = \(\sqrt{(a-0)^2+(0-3)^2}\) = 6
\(\sqrt{a^2+9}\) = 6
a ² + 9 = 36 …[Squaring both the sides
a ² = 36 – 9 = 27 = 3 × 3 × 3
∴ a = ±3√3
∴ Coordinates of the points
A(±3√3, 0) and B(0, 3).

Section – C

Q. No. 41 – 45 are based on Case Study – I, you have to answer any (4) four questions. Q. No. 46 – 50 are based on Case Study – II, you have to answer any (4) four questions.

Case Study – I
A book store shopkeeper gives books on rent for reading. He has variety of books in his store related to fiction, stories and quizzes etc. He takes a fixed charge for the first two days and an additional charge for subsequent day. Amruta paid ₹22 for a book and kept for 6 days; while Radhika paid ₹16 for keeping the book for 4 days.

Assume that the fixed charge be ₹x and additional charge (per day) be ₹y.

Based on the above information, answer any four of the following questions:

Question 41.
The situation of amount paid by Radhika, is algebraically represented by
(a) x – 4y = 16
(b) x + 4y = 16
(c) x – 2y = 16
(d) x + 2y = 16
Answer:
(d) x + 2y = 16
Radhika paid ₹16 for 4 days
ATQ, (Fixed charge for I ^st 2 days) + 2 days charges = 16
∴ x + 2y = 16 ……… (i)

Question 42.
The situation of amount paid by Amruta, is algebraically represented by
(a) x – 2y = 11
(b) x – 2y = 22
(c) x + 4y = 22
(d) x – 4y = 11
Answer:
(c) x + 4y = 22
Amruta paid ₹22 for 6 days
(Fixed charge for I ^st 2 days) + 4 days charges = 22
∴ x + 4y = 22 …(ii)

Question 43.
What are the additional charges for each subsequent day for a book?
(a) ₹6
(b) ₹5
(c) ₹4
(d) ₹3
Answer:
(d) ₹3
Solving (i) and (ii),

∴ y = 3 ……. (iii)
∴ Additional charges = ₹3

Question 44.
What are the fixed charges for a book?
(a) ₹9
(b) ₹10
(c) ₹13
(d) ₹15
Answer:
(b) ₹10
(b) Putting y = 3 from (iii) in (i), we get
⇒ x + 2(3) = 16
∴ x = 16 – 6 = 10 .
∴ Fixed charges = ₹10

Question 45.
What is the total amount paid by both, if both of them have kept the book for 2 more days?
(a) ₹35
(b) ₹52
(c) ₹50
(d) ₹58
Answer:
(c) ₹50
(c) Total amount paid by both
= (22 + 2 y) + (16 + 2y)
= 38 + 4y = 38 + 4(3) …[Point 43
= 38 + 12 = ₹50

Case Study – II

A group of students of class X visited India Gate on an education trip. The teacher and the students had interest in history as well. The teacher narrated that India Gate, official name Delhi Memorial, originally called Alldndia War Memorial, monumental sandstone arch in New Delhi, is dedicated to the troops of British India who died in wars fought between 1914 and 1919. The teacher also said that India Gate, which is located at the eastern end of the Rajpath (formerly called the Kingsway), is about 138 feet (42 metres) in height.
(Use √3 = 1.732)

Based on the above situation, answer any four of the following questions:

Question 46.
What is the angle of elevation if they are standing at a distance of 42 m away from the monument?
(a) 30°
(b) 45°
(c) 60°
(d) 0°
Answer:
(b) 45°
(b) tan θ = \(\frac{P}{B}\) = \(\frac{42}{42}\) = 1
⇒ tan θ = tan 45°
∴ θ = 45°

Question 47.
They want to see the tower at an angle of 60°. So, they want to know the distance where they should stand and hence find the distance.
(a) 24.24 m
(b) 20.12 m
(c) 42 m
(d) 24.64 m
Answer:
(a) 24.24 m
tan 60° = \(\frac{\mathrm{P}}{\mathrm{B}}=\frac{42}{x}\)
⇒ √3 = \(\frac{42}{x}\)
⇒ x = \(\frac{42}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\) = 24.24 m

Question 48.
If the altitude of the Sun is at 60°, then the height of the vertical tower that will cast a shadow of length 20 m is
(a) 20√3 m
(b) \(\frac{20}{\sqrt{3}}\)m
(c) \(\frac{15}{\sqrt{3}}\)m
(d) 15√3 m
Answer:
(a) 20√3 m
tan 60° = \(\frac{h}{20}\)
⇒ √3 = \(\frac{h}{20}\) ∴ h = 20√3 m

Question 49.
The ratio of the length of a rod and its shadow is 1:1. The angle of elevation of the Sun is
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Answer:
(b) 45°
tan θ = \(\frac{1}{1}\) = tan 45°
∴ θ = 45°

Question 50.
The angle formed by the line of sight with the horizontal when the object viewed is below the horizontal level is
(a) corresponding angle
(b) angle of elevation
(c) angle of depression
(d) complete angle
Answer:
(a) corresponding angle

Immerse yourself in the whirlwind of fun that is Crazy Time Live Casino, an interactive online game show that’s all about the excitement of big multipliers and even bigger wins. With its colorful wheel and engaging game hosts, Crazy Time offers a unique blend of entertainment and the chance to multiply your stakes by up to 20,000x.

The game features four thrilling bonus rounds: Cash Hunt, Pachinko, Coin Flip, and the titular Crazy Time, each with its own set of surprises and potential for payout. It’s a live casino experience that keeps you on the edge of your seat, eagerly anticipating where the wheel will stop next.

For a direct path to this exhilarating experience, https://crazytimeshow.com/ is your destination. It’s where the crazy action unfolds, and you can join the fun from anywhere, at any time.

Crazy Time Live Casino isn’t just a game; it’s a spectacle of chance and fortune. Whether you’re a seasoned gambler or new to the scene, it promises a rollercoaster of emotions with every spin. So why not take a chance and see where the crazy time takes you?