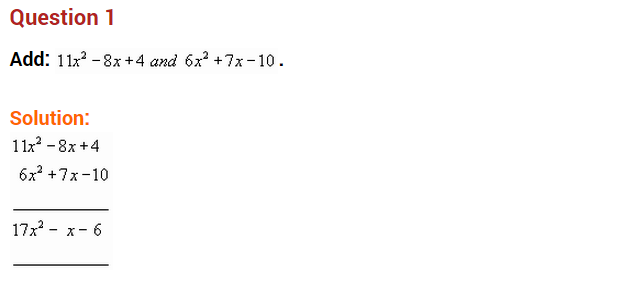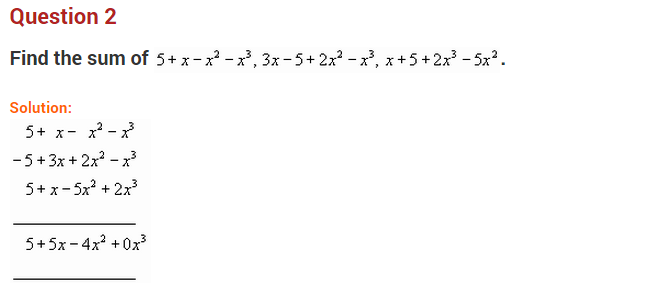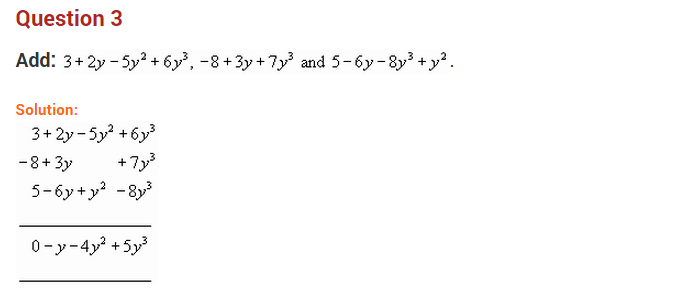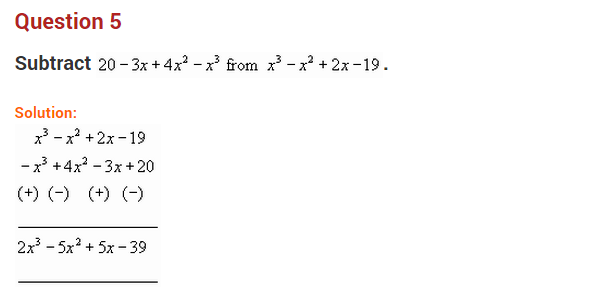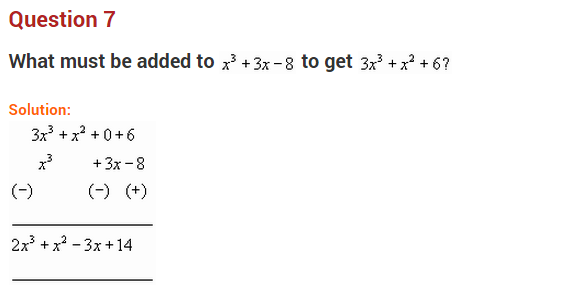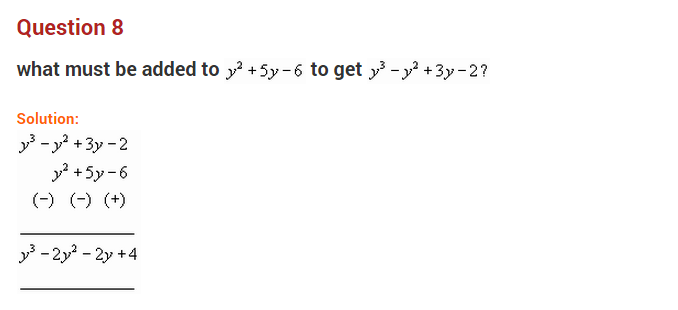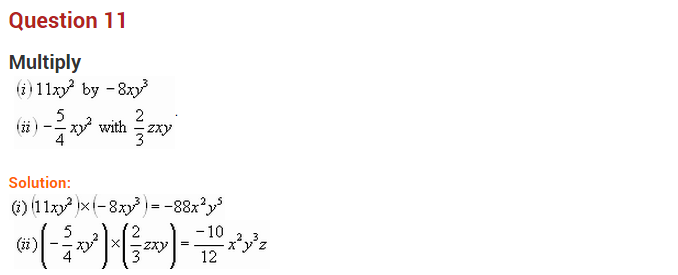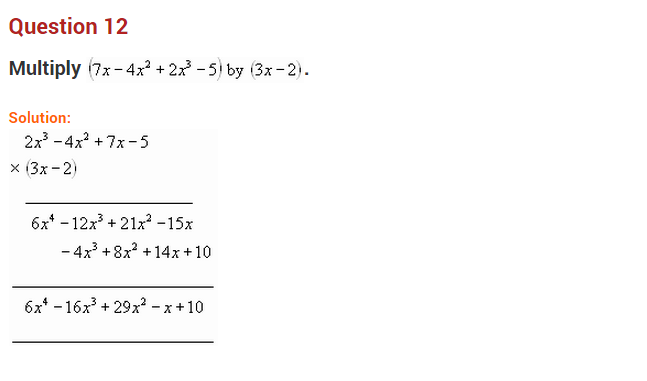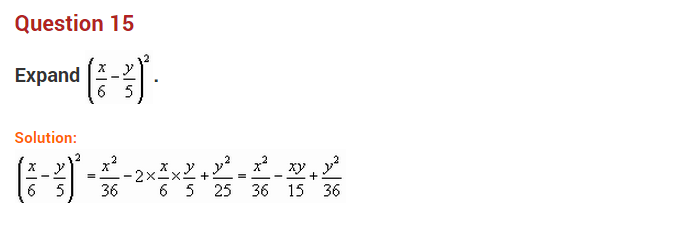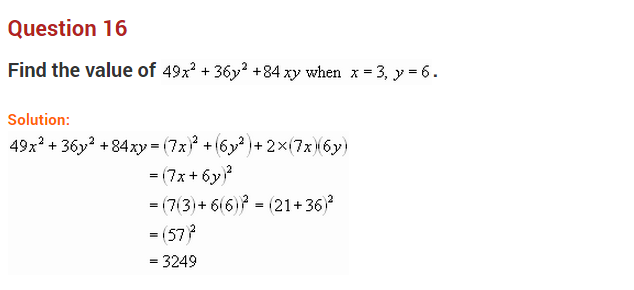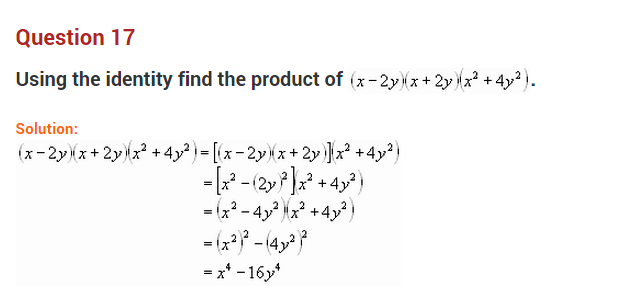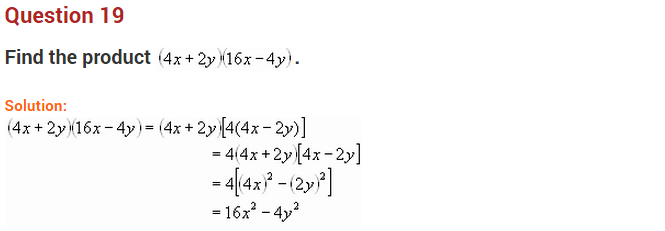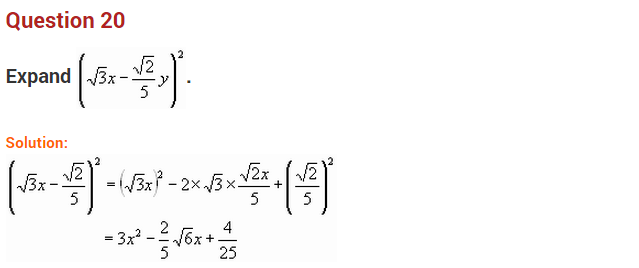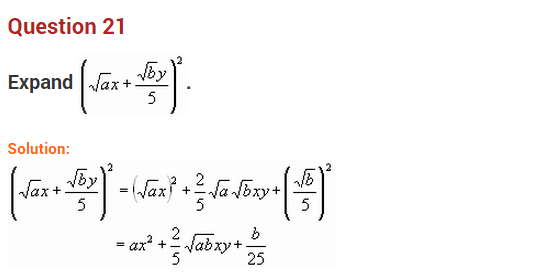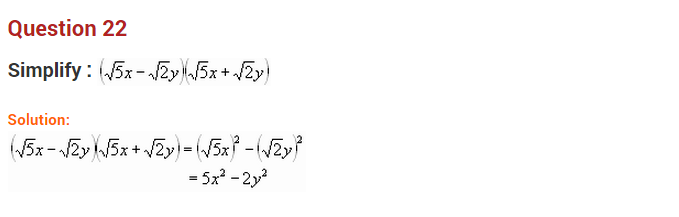Algebraic Expressions and Identities Class 8 Extra Questions Maths Chapter 9

Algebraic Expressions and Identities Class 8 Extra Questions Maths Chapter 9

Extra Questions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities

Algebraic Expressions and Identities Class 8 Extra Questions Very Short Answer Type

Question 1.
Write two examples of each of
(i) Monomials
(ii) Binomials
(iii) Trinomials
Solution:
(i) Monomials:
(a) 3x
(b) 5xy ²
(ii) Binomials:
(a) p + q
(b) -5a + 2b
(iii) Trinomials:
(a) a + b + c
(b) x ² + x + 2

Question 2.
Identify the like expressions.
5x, -14x, 3x ² + 1, x ² , -9x ² , xy, -3xy
Solution:
Like terms: 5x and -14x, x ² and -9x ² , xy and -3xy

Question 3.
Identify the terms and their coefficients for each of the following expressions:
(i) 3x ² y – 5x
(ii) xyz – 2y
(iii) -x – x ²
Solution:

Question 4.
Add: -3a ² b ² , –\(\frac { 5 }{ 2 }\) a ² b ² , 4a ² b ² , \(\frac { 2 }{ 3 }\) a ² b ²
Solution:

Question 5.
Add: 8x ² + 7xy – 6y ² , 4x ² – 3xy + 2y ² and -4x ² + xy – y ²
Solution:

Question 6.
Subtract: (4x + 5) from (-3x + 7)
Solution:
(-3x + 7) – (4x + 5) = -3x + 7 – 4x – 5 = -3x – 4x + 7 – 5 = -7x + 2

Question 7.
Subtract: 3x ² – 5x + 7 from 5x ² – 7x + 9
Solution:
(5x ² – 7x + 9) – (3x ² – 5x + 7)
= 5x ² – 7x + 9 – 3x ² + 5x – 7
= 5x ² – 3x ² + 5x – 7x + 9 – 7
= 2x ² – 2x + 2

Question 8.
Multiply the following expressions:
(a) 3xy ² × (-5x ² y)
(b) \(\frac { 1 }{ 2 }\) x ² yz × \(\frac { 2 }{ 3 }\) xy ² z × \(\frac { 1 }{ 5 }\) x ² yz
Solution:

Question 9.
Find the area of the rectangle whose length and breadths are 3x ² y m and 5xy ² m respectively.
Solution:
Length = 3x ² y m, breadth = 5xy ² m
Area of rectangle = Length × Breadth = (3x ² y × 5xy ² ) sq m = (3 × 5) × x ² y × xy ² sq m = 15x ³ y ³ sq m

Question 10.
Multiply x ² + 7x – 8 by -2y.
Solution:

Algebraic Expressions and Identities Class 8 Extra Questions Short Answer Type

Question 11.
Simplify the following:
(i) a ² (b ² – c ² ) + b ² (c ² – a ² ) + c ² (a ² – b ² )
(ii) x ² (x – 3y ² ) – xy(y ² – 2xy) – x(y ³ – 5x ² )
Solution:
(i) a ² (b ² – c ² ) + b ² (c ² – a ² ) + c ² (a ² – b ² )
= a ² b ² – a ² c ² ) + b ² c ² – b ² a ² ) + c ² a ² – c ² b ² )
= 0
(ii) x ² (x – 3y ² ) – xy(y ² – 2xy) – x(y ³ – 5x ² )
= x ³ – 3x ² y ² – xy ³ + 2x ² y ² – xy ³ + 5x ³
= x ³ + 5x ³ – 3x ² y ² + 2x ² y ² – xy ³ – xy ³
= 6x ³ – x ² y ² – 2xy ³

Question 12.
Multiply (3x ² + 5y ² ) by (5x ² – 3y ² )
Solution:
(3x ² + 5y ² ) × (5x ² – 3y ² )
= 3x ² (5x ² – 3y ² ) + 5y ² (5x ² – 3y ² )
= 15x ⁴ – 9x ² y ² + 25x ² y ² – 15y ⁴
= 15x ⁴ + 16x ² y ² – 15y ⁴

Question 13.
Multiply (6x ² – 5x + 3) by (3x ² + 7x – 3)
Solution:
(6x ² – 5x + 3) × (3x ² + 7x – 3)
= 6x ² (3x ² + 7x – 3) – 5x(3x ² + 7x – 3) + 3(3x ² + 7x – 3)
= 18x ⁴ + 42x ³ – 18x ² – 15x ³ – 35x ² + 15x + 9x ² + 21x – 9
= 18x ⁴ + 42x ³ – 15x ³ – 18x ² – 35x ² + 9x ² + 15x + 21x – 9
= 18x ⁴ + 27x ³ – 44x ² + 36x – 9

Question 14.
Simplify:
2x ² (x + 2) – 3x (x ² – 3) – 5x(x + 5)
Solution:
2x ² (x + 2) – 3x(x ² – 3) – 5x(x + 5)
= 2x ³ + 4x ² – 3x ³ + 9x – 5x ² – 25x
= 2x ³ – 3x ³ – 5x ² + 4x ² + 9x – 25x
= -x ³ – x ² – 16x

Question 15.
Multiply x ² + 2y by x ³ – 2xy + y ³ and find the value of the product for x = 1 and y = -1.
Solution:
(x ² + 2y) × (x ³ – 2xy + y ³ )
= x ² (x ³ – 2xy + y ³ ) + 2y(x ³ – 2xy + y ³ )
= x ⁵ – 2x ³ y + x ² y ³ + 2x ³ y – 4xy ² + 2y ⁴
= x ⁵ + x ² y ³ – 4xy ² + 2y ⁴
Put x = 1 and y = -1
= (1) ⁵ + (1) ² (-1) ³ – 4(1)(-1) ² + 2(-1) ⁴
= 1 + (1) (-1) – 4(1)(1) + 2(1)
= 1 – 1 – 4 + 2
= -2

Question 16.
Using suitable identity find:
(i) 48 ² (NCERT Exemplar)
(ii) 96 ²
(iii) 231 ² – 131 ²
(iv) 97 × 103
(v) 181 ² – 19 ² = 162 × 200 (NCERT Exemplar)
Solution:

Question 17.

Solution:

Question 18.
Verify that (11pq + 4q) ² – (11pq – 4q) ² = 176pq ² (NCERT Exemplar)
Solution:
LHS = (11pq + 4q) ² – (11pq – 4q) ² = (11pq + 4q + 11pq – 4q) × (11pq + 4q – 11pq + 4q)
[using a ² -b ² = (a – b) (a + b), here a = 11pq + 4q and b = 11 pq – 4q]
= (22pq) (8q)
= 176 pq ²
= RHS.
Hence Verified.

Question 19.
Find the value of \(\frac { { 38 }^{ 2 }-{ 22 }^{ 2 } }{ 16 }\), using a suitable identity. (NCERT Exemplar)
Solution:

Question 20.
Find the value of x, if 10000x = (9982) ² – (18) ² (NCERT Exemplar)
Solution:
RHS = (9982) ² – (18) ² = (9982 + 18)(9982 – 18)
[Since a ² -b ² = (a + b) (a – b)]
= (10000) × (9964)
LHS = (10000) × x
Comparing L.H.S. and RHS, we get
10000x = 10000 × 9964
x = 9964

Extra Questions for Class 8 Maths

NCERT Solutions for Class 8 Maths